Question

如圖，AB為⊙O的直徑，弦CD與AB相交于E，DE=EC，過點B的切線與AD的延長線交于F，過E作EG⊥BC于G，延長GE交AD于H．

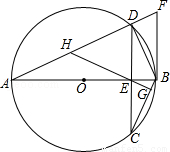
（1）求證：AH=HD；

（2）若cos∠C=，DF=9，求⊙O的半徑．

 

Answer 1

【答案】

解：（1）證明：∵AB為⊙O的直徑，DE=EC，∴AB⊥CD。∴∠C+∠CBE=90°。

∵EG⊥BC，∴∠C+∠CEG=90°。∴∠CBE=∠CEG。

∵∠CBE=∠CDA，∠CEG=∠DEH，∴∠CDA=∠DEH。∴HD=EH。

∵∠A+∠ADC=90°，∠AEH+∠DEH=90°，∴AH=EH。∴AH=HD。

（2）∵AB為⊙O的直徑，∴∠ADB=90°。∴∠BDF=90°。

∵BF是⊙O的切線，∴∠DBF=∠C。

∵cos∠C=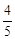，DF=9，∴ 。

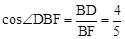設BD=4k，則BF=5k，由勾股定理，得DF=3k。

∴3k=9， k=3。∴BD=4k=12。

∵∠A=∠C，∴sin∠A=。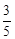

∴。

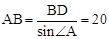∴⊙O的半徑為10

【解析】

試題分析：（1）由AB為⊙O的直徑，DE=EC，根據垂徑定理的推論，從而可證得AB⊥CD，又由EG⊥BC，易證得∠CDA=∠DEH，即可得HD=EH，繼而可證得AH=EH，則可證得結論。

（2）由AB為⊙O的直徑，可得∠BDF=90°，由BF是切線，可得∠DBF=∠C，然后由三角函數的性質，求得BD的長，繼而求得答案。