
【題目】居民區內的“廣場舞”引起媒體關注,小王想了解本小區居民對“廣場舞”的看法,進行了一次抽樣調查,把居民對“廣場舞”的看法分為四個層次:A.非常贊同;B.贊同但要有時間限制;C.無所謂;D.不贊同.并將調查結果繪制了圖1和圖2兩幅不完整的統計圖.

請你根據圖中提供的信息解答下列問題:
(1)求本次被抽查的居民有多少人?
(2)將圖1和圖2補充完整;
(3)估計該小區4000名居民中對“廣場舞”的看法表示贊同(包括A層次和B層次)的大約有多少人.
【答案】(1)300(2)圖形見解析(3)2800
【解析】
試題分析:(1)由被調查人數=A層次的人數÷A層次人數占被調查人數的百分比,計算可得;
(2)根據D層次人數÷被調查總人數=D層次百分比,用1減去其它層次百分比可得B層次百分比,將B、C兩層次百分比分別乘以被調查總人數可得B、C層次的人數,補全圖形;
(3)用A、B兩層次百分比之和乘以總人數4000可得.
試題解析:(1)∵90÷30%=300(人),
∴本次被抽查的居民有300人.
(2)∵D所占的百分比:30÷300=10%,
∴B所占的百分比:1﹣20%﹣30%﹣10%=40%,
∴B對應的人數:300×40%=120(人),C對應的人數:300×20%=60(人),
補全統計圖,如圖所示:
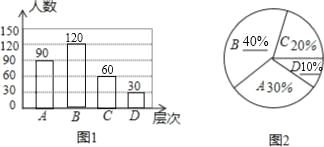
(3)∵4000×(30%+40%)=2800(人),
∴估計該小區4000名居民中對“廣場舞”的看法表示贊同(包括A層次和B層次)的大約有2800人.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】下列有關比例中項的描述正確的有( )
(1)若a,b,c滿足![]() ,則b是a,c的比例中項;
,則b是a,c的比例中項;
(2)實數b是2,8的比例中項,則b=4;
(3)如圖1,點F是EG邊上一點,且∠EDF=∠G,則DE是EF,EG的比例中項;
(4)如圖2,四邊形ABCD中,AD∥BC,兩對角線相交于點O,記△AOD,△ABO,△OBC的面積分別為S1,S2,S3,則S2是S1、S3的比例中項.

A.(2)(3) B.(1)(3)(4) C.(1)(2)(3)(4) D.(1)(3)
查看答案和解析>>
科目:初中數學 來源: 題型:
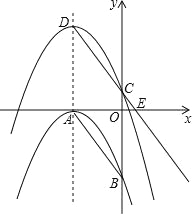
【題目】如圖,拋物線C1:y=﹣![]() (x+3)2與x,y軸分別相交于點A,B,將拋物線C1沿對稱軸向上平移,記平移后的拋物線為C2,拋物線C2的頂點是D,與y軸交于點C,射線DC與x軸相交于點E,
(x+3)2與x,y軸分別相交于點A,B,將拋物線C1沿對稱軸向上平移,記平移后的拋物線為C2,拋物線C2的頂點是D,與y軸交于點C,射線DC與x軸相交于點E,
(1)求A,B點的坐標;
(2)當CE:CD=1:2時,求此時拋物線C2的頂點坐標;
(3)若四邊形ABCD是菱形.
①此時拋物線C2的解析式;
②點F在拋物線C2的對稱軸上,且點F在第三象限,點M在拋物線C2上,點P是坐標平面內一點,是否存在以A,F,P,M為頂點的四邊形與菱形ABCD相似,并且這個菱形以A為頂點的角是鈍角,若存在求出點F的坐標,若不存在請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中,其中正確命題的個數為( )個.
①方差是衡量一組數據波動大小的統計量;②影響超市進貨決策的主要統計量是眾數;③折線統計圖反映一組數據的變化趨勢;④水中撈月是必然事件.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC 中,BD、CE分別是AC、AB上的高,BD與CE交于點O.BE=CD

(1)問△ABC為等腰三角形嗎?為什么?
(2)問點O在∠A的平分線上嗎?為什么?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com