
【題目】張師傅駕車運送荔枝到某地出售,汽車出發前油箱有油50升,行駛若干小時后,圖中在加油站加油若干升,油箱中剩余油量y(升)與行駛時間t(小時)之間的關系如圖所示. 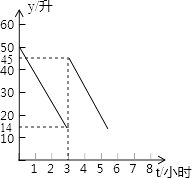
(1)汽車行駛小時后加油,中途加油升;
(2)求加油前油箱剩余油量y與行駛時間t的函數關系式;
(3)已知加油前、后汽車都以70千米/小時勻速行駛,如果加油站距目的地210千米,要到達目的地,問油箱中的油是否夠用?請說明理由.
 53隨堂測系列答案
53隨堂測系列答案科目:初中數學 來源: 題型:
【題目】一個不透明的口袋中裝有4個分別標有數1,2,3,4的小球,它們的形狀、大小完全相同,小紅先從口袋里隨機摸出一個小球記下數為x,小穎在剩下的3個球中隨機摸出一個小球記下數為y,這樣確定了點P的坐標(x,y).
(1)小紅摸出標有數3的小球的概率是 .
(2)請你用列表法或畫樹狀圖法求點P(x,y)在函數y=﹣x+5圖象上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD是正方形,E、F分別是DC和CB的延長線上的點,且DE=BF,連接AE、AF、EF. 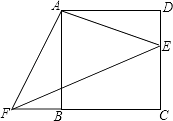
(1)求證:△ADE≌△ABF;
(2)若BC=8,DE=6,求△AEF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,以△ABC的邊AB、AC為邊分別向外作等腰直角△ABD和等腰直角△ACE,連接CD、BE、DE 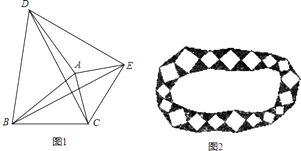
(1)證明:△ADC≌△ABE;
(2)試判斷△ABC與△ADE面積之間的關系,并說明理由;
(3)園林小路,曲徑通幽,如圖2所示,小路由白色的正方形大理石和黑色的三角形大理石鋪成,已知中間的所有正方形的面積之和是a平方米,內圈的所有三角形的面積之和是b平方米,這條小路一共占地平方米.(不用寫過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=10,點D是邊BC上一動點(不與B,C重合),∠ADE=∠B=α,DE交AC于點E,且cosα= ![]() .下列結論:①△ADE∽△ACD;②當BD=6時,△ABD與△DCE全等;③△DCE為直角三角形時,BD為8;④0<CE≤6.4.其中正確的結論是 . (把你認為正確結論的序號都填上)
.下列結論:①△ADE∽△ACD;②當BD=6時,△ABD與△DCE全等;③△DCE為直角三角形時,BD為8;④0<CE≤6.4.其中正確的結論是 . (把你認為正確結論的序號都填上) 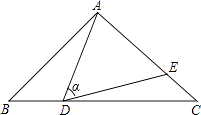
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=3,BC=4,點F在邊AC上,并且CF=1,點E為邊BC上的動點,將△CEF沿直線EF翻折,點C落在點P處,則點P到邊AB距離的最小值是 . 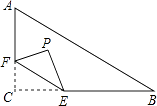
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】愛好思考的小茜在探究兩條直線的位置關系查閱資料時,發現了“中垂三角形”,即兩條中線互相垂直的三角形稱為“中垂三角形”.如圖(1)、圖(2)、圖(3)中,AM、BN是△ABC的中線,AM⊥BN于點P,像△ABC這樣的三角形均為“中垂三角形”.設BC=a,AC=b,AB=c.
(1)【特例探究】
如圖1,當tan∠PAB=1,c=4 ![]() 時,a= , b=;
時,a= , b=;
如圖2,當∠PAB=30°,c=2時,a= , b=;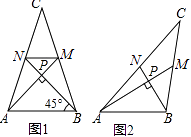
(2)【歸納證明】
請你觀察(1)中的計算結果,猜想a2、b2、c2三者之間的關系,用等式表示出來,并利用圖3證明你的結論.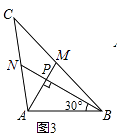
(3)【拓展證明】
如圖4,ABCD中,E、F分別是AD、BC的三等分點,且AD=3AE,BC=3BF,連接AF、BE、CE,且BE⊥CE于E,AF與BE相交點G,AD=3 ![]() ,AB=3,求AF的長.
,AB=3,求AF的長.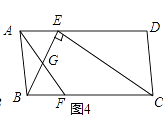
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明參加某個智力競答節目,答對最后兩道單選題就順利通關.第一道單選題有3個選項,第二道單選題有4個選項,這兩道題小明都不會,不過小明還有一個“求助”沒有用(使用“求助”可以讓主持人去掉其中一題的一個錯誤選項).
(1)如果小明第一題不使用“求助”,那么小明答對第一道題的概率是 .
(2)如果小明將“求助”留在第二題使用,請用樹狀圖或者列表來分析小明順利通關的概率.
(3)從概率的角度分析,你建議小明在第幾題使用“求助”.(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,下列結論:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正確的個數是( ) 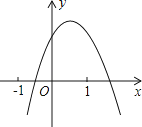
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com