
【題目】如圖,在平面直角坐標系中,已知![]() 的三個頂點的坐標分別為
的三個頂點的坐標分別為![]() ,
,![]() ,
,![]()
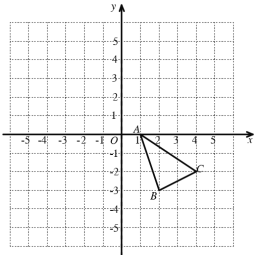
(1)畫出![]() 關于
關于![]() 軸的對稱圖形
軸的對稱圖形![]() ,畫出
,畫出![]() 向左平移3個單位長度后得到的
向左平移3個單位長度后得到的![]() ,
,
(2)如果![]() 上有一點
上有一點![]() 經過上述兩次變換,那么對應
經過上述兩次變換,那么對應![]() 上的點
上的點![]() 的坐標是______
的坐標是______
科目:初中數學 來源: 題型:
【題目】閱讀以下文字并解決問題:對于形如![]() 這樣的二次三項式,我們可以直接用公式法把它分解成
這樣的二次三項式,我們可以直接用公式法把它分解成![]() 的形式,但對于二次三項式
的形式,但對于二次三項式![]() ,就不能直接用公式法分解了.此時,我們可以在
,就不能直接用公式法分解了.此時,我們可以在![]() 中間先加上一項
中間先加上一項![]() ,使它與
,使它與![]() 的和構成一個完全平方式,然后再減去
的和構成一個完全平方式,然后再減去![]() ,則整個多項式的值不變.即:
,則整個多項式的值不變.即: ,像這樣,把一個二次三項式變成含有完全平方式的形式的方法,叫做配方法.
,像這樣,把一個二次三項式變成含有完全平方式的形式的方法,叫做配方法.
![]() 利用“配方法”因式分解:
利用“配方法”因式分解:![]()
![]() 如果
如果![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=CB,∠ABC=90°,D為AB延長線上一點,點E在BC邊上,且BE=BD,連結AE、DE、DC

①求證:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:如圖1,在平面直角坐標系中,點M是二次函數![]() 圖象上一點,過點M作
圖象上一點,過點M作![]() 軸,如果二次函數
軸,如果二次函數![]() 的圖象與
的圖象與![]() 關于l成軸對稱,則稱
關于l成軸對稱,則稱![]() 是
是![]() 關于點M的伴隨函數
關于點M的伴隨函數![]() 如圖2,在平面直角坐標系中,二次函數
如圖2,在平面直角坐標系中,二次函數![]() 的函數表達式是
的函數表達式是![]() ,點M是二次函數
,點M是二次函數![]() 圖象上一點,且點M的橫坐標為m,二次函數
圖象上一點,且點M的橫坐標為m,二次函數![]() 是
是![]() 關于點M的伴隨函數.
關于點M的伴隨函數.



![]() 若
若![]() ,
,
![]() 求
求![]() 的函數表達式.
的函數表達式.
![]() 點
點![]() ,
,![]() 在二次函數
在二次函數![]() 的圖象上,若
的圖象上,若![]() ,a的取值范圍為______.
,a的取值范圍為______.
![]() 過點M作
過點M作![]() 軸,
軸,
![]() 如果
如果![]() ,線段MN與
,線段MN與![]() 的圖象交于點P,且MP:
的圖象交于點P,且MP:![]() :3,求m的值.
:3,求m的值.
![]() 如圖3,二次函數
如圖3,二次函數![]() 的圖象在MN上方的部分記為
的圖象在MN上方的部分記為![]() ,剩余的部分沿MN翻折得到
,剩余的部分沿MN翻折得到![]() ,由
,由![]() 和
和![]() 所組成的圖象記為
所組成的圖象記為![]() .以
.以![]() 、
、![]() 為頂點在x軸上方作正方形
為頂點在x軸上方作正方形![]() 直接寫出正方形ABCD與G有三個公共點時m的取值范圍.
直接寫出正方形ABCD與G有三個公共點時m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() ,
,![]() 的延長線與
的延長線與![]() 相交于點
相交于點![]() ,連接
,連接![]() 、
、![]() .
.
![]() 如圖
如圖![]() ,若
,若![]() ,
,![]() .
.
①求證:![]() ;②猜想線段
;②猜想線段![]() 、
、![]() 的數量關系,并證明你的猜想;
的數量關系,并證明你的猜想;
![]() 如圖
如圖![]() ,若
,若![]() ,
,![]() (
(![]() 為常數),求
為常數),求![]() 的值(用含
的值(用含![]() 、
、![]() 的式子表示).
的式子表示).

查看答案和解析>>
科目:初中數學 來源: 題型:
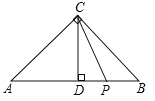
【題目】如圖,在△ABC中,∠ACB=90°,∠A=45°,CD⊥AB于點D,點P在線段DB上,若AP2-PB2=48,則△PCD的面積為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
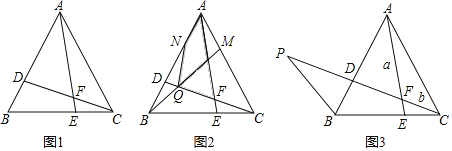
【題目】如圖,點D,E分別在正△ABC的邊AB,BC上,且BD=CE,CD,AE交于點F.
(1)①求證:△ACE≌△CBD;②求∠AFD的度數;
(2)如圖2,若D,E,M,N分別是△ABC各邊上的三等分點,BM,CD交于Q.若△ABC的面積為S,請用S表示四邊形ANQF的面積 ;
(3)如圖3,延長CD到點P,使∠BPD=30°,設AF=a,CF=b,請用含a,b的式子表示PC長,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
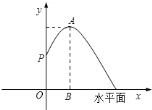
【題目】某市人民廣場上要建造一個圓形的噴水池,并在水池中央垂直安裝一個柱子![]() ,柱子頂端
,柱子頂端![]() 處裝上噴頭,由
處裝上噴頭,由![]() 處向外噴出的水流(在各個方向上)沿形狀相同的拋物線路徑落下(如圖所示).若已知
處向外噴出的水流(在各個方向上)沿形狀相同的拋物線路徑落下(如圖所示).若已知![]() 米,噴出的水流的最高點
米,噴出的水流的最高點![]() 距水平面的高度是
距水平面的高度是![]() 米,離柱子
米,離柱子![]() 的距離為
的距離為![]() 米.
米.
![]() 求這條拋物線的解析式;
求這條拋物線的解析式;
![]() 若不計其它因素,水池的半徑至少要多少米,才能使噴出的水流不至于落在池外?
若不計其它因素,水池的半徑至少要多少米,才能使噴出的水流不至于落在池外?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:已知在△ABC中,AB=AC,D為BC邊的中點,過點D作DE⊥AB,DF⊥AC,垂足分別為E,F.

(1)求證:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com