
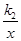 (k2>0)的交
(k2>0)的交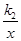 (k2>0)于點N.當
(k2>0)于點N.當 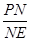 取最大值時,若PN=
取最大值時,若PN= 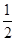 ,求此時雙曲線的解析式.
,求此時雙曲線的解析式.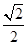 )(2)y=
)(2)y=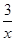
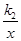 (k2>0)上,
(k2>0)上,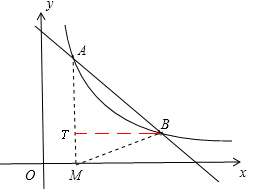
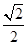 。
。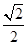 )。
)。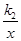 (k2>0)的交點,
(k2>0)的交點,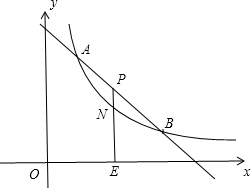
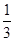 k2,b=
k2,b=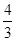 k2。
k2。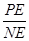 =
=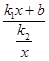 =
=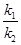 x2+
x2+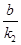 x=-
x=-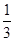 x2+
x2+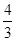 x。
x。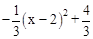
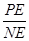 =1,又∵當x=2時,
=1,又∵當x=2時, 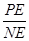 的最大值是
的最大值是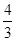 。
。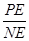 ≤
≤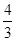 .。∴ PE≥NE。
.。∴ PE≥NE。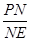 =
=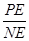 -1=
-1=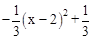 。
。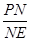 的最大值是
的最大值是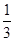 。
。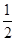 ,∴ NE=
,∴ NE=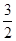 。∴ 點N(2,
。∴ 點N(2,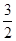 ) 。 ∴ k2=3。
) 。 ∴ k2=3。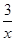 。
。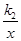 (k2>0)上,得到c=3d,則A點坐標為(1,3d),在Rt△BTM中應用勾股定理即可計算出d的值,即可確定B點坐標。
(k2>0)上,得到c=3d,則A點坐標為(1,3d),在Rt△BTM中應用勾股定理即可計算出d的值,即可確定B點坐標。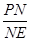 關于x的二次函數,應用二次函數的最值即可求得
關于x的二次函數,應用二次函數的最值即可求得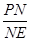 的最大值,此時根據PN=
的最大值,此時根據PN=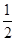 求得NE=
求得NE=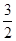 ,從而得到N(2,
,從而得到N(2,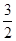 ),代入y=
),代入y=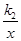 即可求得k2=3。因此求得反比例函數的解析式為y=
即可求得k2=3。因此求得反比例函數的解析式為y=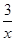


 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案科目:初中數學 來源:不詳 題型:解答題
 中,直線AB分別與
中,直線AB分別與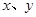 軸交于點B、A,與反比例函數的圖象分別交于點C、D,CE⊥
軸交于點B、A,與反比例函數的圖象分別交于點C、D,CE⊥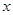 軸于點E,點C坐標是(-2,3),點D的坐標是(6,n).
軸于點E,點C坐標是(-2,3),點D的坐標是(6,n).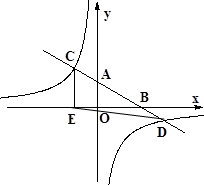
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 和一次函數y=2x-1,其中一次函數的圖象經過(a,b),(a+1,b+k)兩點.
和一次函數y=2x-1,其中一次函數的圖象經過(a,b),(a+1,b+k)兩點.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
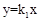 與反比例函數
與反比例函數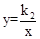 的圖象相交于點A、B兩點,若點A的坐標為(2,1),則點B的坐標是【 】
的圖象相交于點A、B兩點,若點A的坐標為(2,1),則點B的坐標是【 】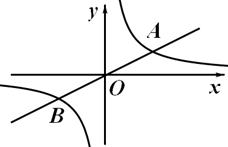
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
 小時,這種顯示器工作的天數為d(天),平均每天工作的時間為t(小時),那么能正確表示d與t之間的函數關系的圖象是( )
小時,這種顯示器工作的天數為d(天),平均每天工作的時間為t(小時),那么能正確表示d與t之間的函數關系的圖象是( )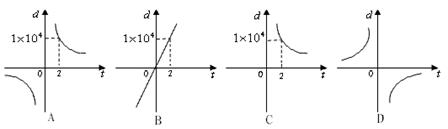
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com