
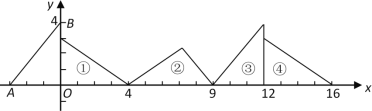
【題目】如圖,在直角坐標系中,已知點![]() ,
,![]() ,對△
,對△![]() 連續作旋轉變換,依次得到三角形①、②、③、④…,則連續作旋轉變第10的三角形的直角頂點的坐標為____.連續作旋轉變第2011的第號三角形的直角頂點的坐標為____.
連續作旋轉變換,依次得到三角形①、②、③、④…,則連續作旋轉變第10的三角形的直角頂點的坐標為____.連續作旋轉變第2011的第號三角形的直角頂點的坐標為____.
【答案】(36,0) (8040,0)
【解析】
觀察不難發現,每三次旋轉為一個循環組依次循環,第10個直角三角形的直角頂點與第9個直角三角形的直角頂點重合,然后求出一個循環組旋轉過的距離,即可得解.
∵A(-3,0),B(0,4),
∴AB=![]() ,
,
由原圖到圖③,相當于向右平移了12個單位長度,三角形④的直角頂點的坐標為(12,0),
這樣旋轉9次直角頂點是(36,0),再旋轉一次到三角形⑩,直角頂點仍然是(36,0),
∵2011=670×3+1
∴轉到第2011次的直角頂點與轉到2010次的直角頂點重合,即(670×12,0)
∴連續作旋轉變到第2011號三角形的直角頂點的坐標為(8040,0)
故答案為:(36,0),(8040,0)


科目:初中數學 來源: 題型:
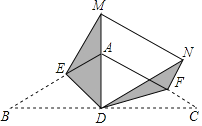
【題目】如圖,在等腰△ABC中,AB=AC=2,∠ABC=30°,AD為BC邊上的高,E、F分別為AB、AC邊上的點,將△ABC分別沿DE、DF折疊,使點B落在DA的延長線上點M處,點C落在點N處,連接MN,若MN∥AC,則AF的長是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“防疫有我,愛衛同行”,為切實開展愛國衛生運動,某校決定在校園組織系列衛生清掃活動,參加人員從全校各部門自愿報名的教師中隨機抽取.數學組有![]() 位教師報名參加第一次清掃活動,
位教師報名參加第一次清掃活動,![]() 位教師分別記為甲、乙、丙、丁.
位教師分別記為甲、乙、丙、丁.
(1)如果需從這![]() 位教師中隨機抽取
位教師中隨機抽取![]() 名教師,求抽到教師甲的概率;
名教師,求抽到教師甲的概率;
(2)如果需從這![]() 位教師中隨機抽取
位教師中隨機抽取![]() 名教師,請用列表或畫樹狀圖的方法,求出抽到教師乙和丁的概率.
名教師,請用列表或畫樹狀圖的方法,求出抽到教師乙和丁的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
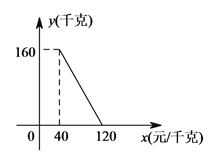
【題目】某商店以40元/千克的單價新進一批茶葉,經調查發現,在一段時間內,銷售量y(千克)與銷售單價x(元/千克)之間的函數關系如圖所示.
(1)根據圖象,求y與x的函數關系式;
(2)商店想在銷售成本不超過3000元的情況下,使銷售利潤達到2400元,問銷售單價應定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 是⊙O的直徑,
是⊙O的直徑,![]() ,點
,點![]() 在⊙O的半徑
在⊙O的半徑![]() 上運動,
上運動,![]() ,垂足為
,垂足為![]() ,
,![]() ,
,![]() 為⊙O的切線,切點為
為⊙O的切線,切點為![]() .
.
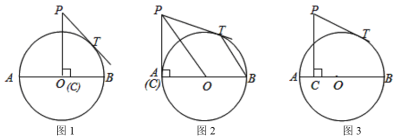
(1)如圖1,當![]() 點運動到
點運動到![]() 點時,求
點時,求![]() 的長;
的長;
(2)如圖2,當![]() 點運動到
點運動到![]() 點時,連接
點時,連接![]() 、
、![]() ,求證:
,求證:![]() ∥
∥![]() ;
;
(3)如圖3,設![]() ,
,![]() ,求y與x的解析式并求出y的最小值.
,求y與x的解析式并求出y的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖
(1)方法體驗:
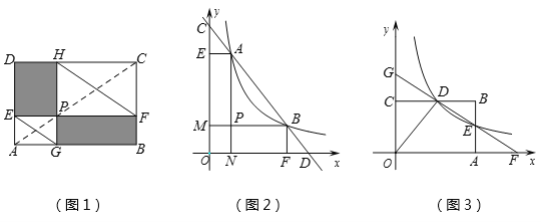
如圖1,點P在矩形ABCD的對角線AC上,且不與點A,C重合,過點P分別作邊AB,AD的平行線,交兩組對邊于點E,F和G,H,容易證明四邊形PEDH和四邊形PFBG是面積相等的矩形,分別連結EG,FH.
①根據矩形PEDH和矩形PFBG面積相等的關系,那么PE·PH= .
②求證:EG∥FH.
(2)方法遷移:
如圖2,已知直線 ![]() 分別與x軸,y軸交于D,C兩點,與雙曲線
分別與x軸,y軸交于D,C兩點,與雙曲線 ![]() 交于A,B兩點. 求證:AC=BD.
交于A,B兩點. 求證:AC=BD.
(3)知識應用:
如圖3,反比例函數 ![]() (x>0)的圖象與矩形ABCO的邊BC交于點D,與邊AB交于點E, 直線DE與x軸,y軸分別交于點F,G .若矩形ABCO的面積為10,△ODG與△ODF的面積比為3:5,則k=________.
(x>0)的圖象與矩形ABCO的邊BC交于點D,與邊AB交于點E, 直線DE與x軸,y軸分別交于點F,G .若矩形ABCO的面積為10,△ODG與△ODF的面積比為3:5,則k=________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某農戶要改造部分農田種植蔬菜.經調查,改造農田費用(元)與改造面積(畝)成正比,比例系數為900,添加輔助設備費用(元)與改造面積(畝)的平方成正比,比例系數為18,以上兩項費用三年內不需再投入;每畝種植蔬菜還需種子、人工費用600元.這項費用每年均需再投入.除上述費用外,沒有其他費用.設改造![]() 畝,每畝蔬菜年銷售額為
畝,每畝蔬菜年銷售額為![]() 元.
元.
(1)設改造當年收益為![]() 元,用含
元,用含![]() ,
,![]() 的式子表示
的式子表示![]() ;
;
(2)按前三年計算,若![]() ,是否改造面積越大收益越大?改造面積為多少時,可以得到最大收益?
,是否改造面積越大收益越大?改造面積為多少時,可以得到最大收益?
(3)按前三年計算,若![]() ,當收益不低于43200元時,求改造面積
,當收益不低于43200元時,求改造面積![]() 的取值范圍.
的取值范圍.
注:收益![]() 銷售額
銷售額![]() (改造費
(改造費![]() 輔助設備費
輔助設備費![]() 種子、人工費).
種子、人工費).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是平行四邊形,![]() //
//![]() ,且分別交對角線AC于點E,F,連接BE,DF.
,且分別交對角線AC于點E,F,連接BE,DF.
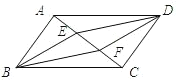
(1)求證:AE=CF;
(2)若BE=DE,求證:四邊形EBFD為菱形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com