【題目】如圖，AB是垂直于水平面的建筑物.為測量AB的高度，小紅從建筑物底端B點出發，沿水平方向行走了5.2米到達點C，然后沿斜坡CD前進，到達坡頂D點處，DC=BC.在點D處放置測角儀，測角儀支架DE高度為0.8米，在E點處測得建筑物頂端A點的仰角∠AEF為27°(點A，B，C，D，E在同一平面內).斜坡CD的坡度(或坡比)i=1：2.4，求建筑物AB的高度.(參考數據sin27°≈0.45，cos27°≈0.89，tan27°≈0.51)
口算能手系列答案科目：初中數學 來源： 題型：
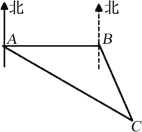
【題目】如圖，專業救助船“滬救1”輪、“滬救2”輪分別位于A、B兩處，同時測得事發地點C在A的南偏東60°且C在B的南偏東30°上．已知B在A的正東方向，且相距100里，請分別求出兩艘船到達事發地點C的距離．（注：里是海程單位，相當于一海里．結果保留根號）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面內容：我們已經學習了《二次根式》和《乘法公式》，聰明的你可以發現：當
，
時，∵
，∴
，當且僅當
時取等號．請利用上述結論解決以下問題：
(1)當
時，
的最小值為_______；當
時，的最大值為__________．
(2)當時，求
的最小值．
(3)如圖，四邊形ABCD的對角線AC ，BD相交于點O，△AOB、△COD的面積分別為4和9，求四邊形ABCD面積的最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
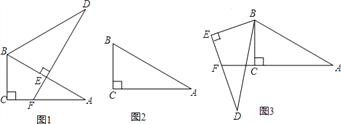
【題目】將兩個全等的直角三角形ABC和DBE按圖①方式擺放，其中∠ACB=∠DEB=90°，∠A=∠D=30°，點E落在AB上，DE所在直線交AC所在直線于點F．
（1）求證：AF+EF=DE；
（2）若將圖①中的△DBE繞點B按順時針方向旋轉角α，且0°＜α＜60°，其它條件不變，請在圖②中畫出變換后的圖形，并直接寫出你在（1）中猜想的結論是否仍然成立；
（3）若將圖①中的△DBE繞點B按順時針方向旋轉角β，且60°＜β＜180°，其它條件不變，如圖③．你認為（1）中猜想的結論還成立嗎？若成立，寫出證明過程；若不成立，請寫出AF、EF與DE之間的關系，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
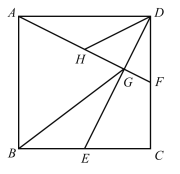
【題目】如圖，在邊長為4的正方形
中，點
、
分別是
、
的中點，
、
交于點
，的中點為
，連接
、
．給出下列結論：①
；②
；③
；④
．其中正確的結論有________．（請填上所有正確結論的序號）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】河南省開封市鐵塔始建于公元1049年（北宋皇祐元年），是國家重點保護文物之一，在900多年中，歷經了數次地震、大風、水患而巍然屹立，素有“天下第一塔”之稱．如圖，小明在鐵塔一側的水平面上一個臺階的底部A處測得塔頂P的仰角為45°，走到臺階頂部B處，又測得塔頂P的仰角為38.7°，已知臺階的總高度BC為3米，總長度AC為10米，試求鐵塔的高度．（結果精確到1米，參考數據：sin38.7°≈0.63，cos38.7°≈0.78，tan38.7°≈0.80）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖， 在平面直角坐標系中， 
的頂點
與原點重合，點
在
軸的正半軸上，
按以下步驟作圖：①以點為圓心，適當長度為半徑作
弧，分別交邊
，
于點
，
；②分別以點，為圓心，大于
的長為半徑作弧， 兩弧在
內交于點
；③作射線
，交邊
于點
．若
，
，則點的坐標為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校“校園主持人大賽”結束后，將所有參賽選手的比賽成績（得分均為整數）進行整理，并分別繪制成扇形統計圖和頻數直方圖．部分信息如下：
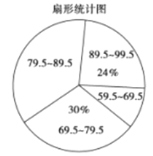
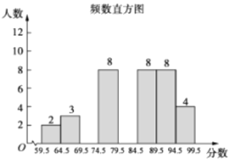
（1）本次比賽參賽選手共有________人，扇形統計圖中“79.5~89.5”這一范圍的人數占總參賽人數的百分比為________；
（2）補全圖2頻數直方圖；
（3）賽前規定，成績由高到低前40%的參賽選手獲獎．某參賽選手的比賽成績為88分，試判斷他能否獲獎，并說明理由；
（4）成績前四名是2名男生和2名女生，若他們中任選2人作為該校文藝晚會的主持人，試求恰好選中1男1女為主持人的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
