
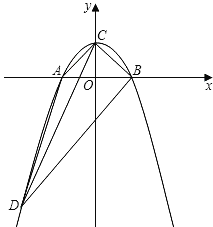
【題目】如圖,拋物線y=ax2+bx+1與x軸交于兩點A(﹣1,0),B(1,0),與y軸交于點C.
(1)求拋物線的解析式;
(2)過點B作BD∥CA拋物線交于點D,求四邊形ACBD的面積;
(3)在x軸下方的拋物線上是否存在點M,過M作MN⊥x軸于點N,使以A、M、N為頂點的三角形與△BCD相似?若存在,則求出點M的坐標;若不存在,請說明理由.
【答案】(1)y=﹣x2+1;(2)4;(3)M (![]() ,﹣
,﹣![]() )或(4,﹣15)或(﹣2,﹣3).
)或(4,﹣15)或(﹣2,﹣3).
【解析】
(1)將A、B的坐標代入拋物線的解析式中,即可求出待定系數的值;
(2)先求出直線AC的解析式,由于BD∥AC,那么直線BD的斜率與直線AC的相同,可據此求出直線BD的解析式,聯立拋物線的解析式即可求出D點的坐標;由圖知四邊形ACBD的面積是△ABC和△ABD的面積和,由此可求得其面積;
(3)易知OA=OB=OC=1,那么△ACB是等腰直角三角形,由于AC∥BD,則∠CBD=90°;根據B、C的坐標可求出BC、BD的長,進而可求出它們的比例關系;若以A、M、N為頂點的三角形與△BCD相似,那么兩個直角三角形的對應直角邊應該成立,可據此求出△AMN兩條直角邊的比例關系,連接拋物線的解析式即可求出M點的坐標.
解:(1)依題意,得:![]() ,解得
,解得![]() ;
;
∴拋物線的解析式為:y=﹣x2+1;
(2)易知A(﹣1,0),C(0,1),則直線AC的解析式為:y=x+1;
由于AC∥BD,可設直線BD的解析式為y=x+h,則有:1+h=0,h=﹣1;
∴直線BD的解析式為y=x﹣1;聯立拋物線的解析式得:
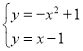 ,解得
,解得![]() ,
,![]() ;
;
∴D(﹣2,﹣3);
∴S四邊形ACBD=S△ABC+S△ABD=![]() ×2×1+
×2×1+![]() ×2×3=4;
×2×3=4;
(3)∵OA=OB=OC=1,
∴△ABC是等腰Rt△;
∵AC∥BD,
∴∠CBD=90°;
易求得BC=![]() ,BD=3
,BD=3![]() ;
;
∴BC:BD=1:3;
由于∠CBD=∠MNA=90°,若以A、M、N為頂點的三角形與△BCD相似,則有:
△MNA∽△CBD或△MNA∽△DBC,得:
![]() 或
或![]() ;
;
即MN=![]() AN或MN=3AN;
AN或MN=3AN;
設M點的坐標為(x,﹣x2+1),
①當x>1時,AN=x﹣(﹣1)=x+1,MN=x2﹣1;
∴x2﹣1=![]() (x+1)或x2﹣1=3(x+1),
(x+1)或x2﹣1=3(x+1),
解得x=![]() ,x=﹣1(舍去)或x=4,x=﹣1(舍去);
,x=﹣1(舍去)或x=4,x=﹣1(舍去);
∴M點的坐標為:M(![]() ,﹣
,﹣![]() )或(4,﹣15);
)或(4,﹣15);
②當x<﹣1時,AN=﹣1﹣x,MN=x2﹣1;
∴x2﹣1=![]() (﹣x﹣1)或x2﹣1=3(﹣x﹣1),
(﹣x﹣1)或x2﹣1=3(﹣x﹣1),
解得x=![]() ,x=﹣1(兩個都不合題意,舍去)或x=﹣2,x=﹣1(舍去);
,x=﹣1(兩個都不合題意,舍去)或x=﹣2,x=﹣1(舍去);
∴M(﹣2,﹣3);
故存在符合條件的M點,且坐標為:M(![]() ,﹣
,﹣![]() )或(4,﹣15)或(﹣2,﹣3).
)或(4,﹣15)或(﹣2,﹣3).


科目:初中數學 來源: 題型:
【題目】(2013年四川綿陽12分)如圖,已知矩形OABC中,OA=2,AB=4,雙曲線![]() (k>0)與矩形兩邊AB、BC分別交于E、F.
(k>0)與矩形兩邊AB、BC分別交于E、F.

(1)若E是AB的中點,求F點的坐標;
(2)若將△BEF沿直線EF對折,B點落在x軸上的D點,作EG⊥OC,垂足為G,證明△EGD∽△DCF,并求k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
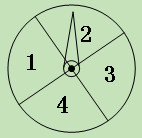
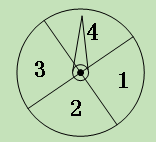
【題目】(11·孝感)學生甲與學生乙玩一種轉盤游戲.如圖是兩個完全相同的轉盤,每個轉盤被分成面積相等的四個區域,分別用數字“1”、“2”、“3”、“4”表示.固定指針,同時轉動兩個轉盤,任其自由停止,若兩指針所指數字的積為奇數,則甲獲勝;若兩指針所指數字的積為偶數,則乙獲勝;若指針指向扇形的分界線,則都重轉一次.在該游戲中乙獲勝的概率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
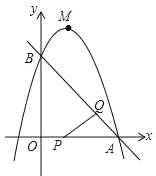
【題目】如圖,已知直線y=﹣x+3與x軸、y軸分別交于A,B兩點,拋物線y=﹣x2+bx+c經過A,B兩點,點P在線段OA上,從點A以1個單位/秒的速度勻速運動;同時,點Q在線段AB上,從點A出發,向點B以![]() 個單位/秒的速度勻速運動,連接PQ,設運動時間為t秒.
個單位/秒的速度勻速運動,連接PQ,設運動時間為t秒.
(1)求拋物線的解析式;
(2)當t為何值時,△APQ為直角三角形;
(3)過點P作PE∥y軸,交AB于點E,過點Q作QF∥y軸,交拋物線于點F,連接EF,當EF∥PQ時,求點F的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系xOy中,點A的坐標為(﹣2,2),點B的坐標為(6,6),拋物線經過A、O、B三點,連結OA、OB、AB,線段AB交y軸于點E.
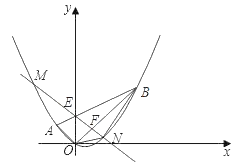
(1)求點E的坐標;
(2)求拋物線的函數解析式;
(3)點F為線段OB上的一個動點(不與點O、B重合),直線EF與拋物線交于M、N兩點(點N在y軸右側),連結ON、BN,當點F在線段OB上運動時,求△BON面積的最大值,并求出此時點N的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數與反比例函數的圖象交于點A(-4,-2)和B(a,4),直線AB交y輸于點C,連接QA、OB.
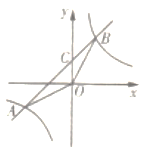
(1)求反比例函數的解析式和點B的坐標:
(2)根據圖象回答,當x的取值在什么范圍內時,一次函數的值大于反比例函數的值;
(3)求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在如圖所示的平面直角坐標系中,已知點A(﹣3,﹣3),點B(﹣1,﹣3),點C(﹣1,﹣1)
(1)畫出△ABC;
(2)以點C為旋轉中心,畫出將△ABC順時針旋轉90度的△A1B1C,并求出線段CA掃過的面積;
(3)以O為位似中心,在第一象限內作出△A2B2C2使△A2B2C2與△ABC位似,且位似比為2,并寫出A2點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
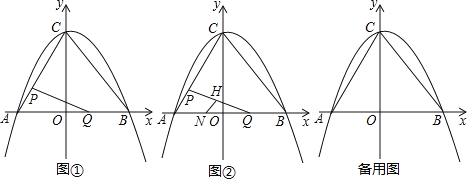
【題目】如圖①,在平面直角坐標系中,二次函數y=﹣![]() x2+bx+c的圖象與坐標軸交于A,B,C三點,其中點A的坐標為(﹣3,0),點B的坐標為(4,0),連接AC,BC.動點P從點A出發,在線段AC上以每秒1個單位長度的速度向點C作勻速運動;同時,動點Q從點O出發,在線段OB上以每秒1個單位長度的速度向點B作勻速運動,當其中一點到達終點時,另一點隨之停止運動,設運動時間為t秒.連接PQ.
x2+bx+c的圖象與坐標軸交于A,B,C三點,其中點A的坐標為(﹣3,0),點B的坐標為(4,0),連接AC,BC.動點P從點A出發,在線段AC上以每秒1個單位長度的速度向點C作勻速運動;同時,動點Q從點O出發,在線段OB上以每秒1個單位長度的速度向點B作勻速運動,當其中一點到達終點時,另一點隨之停止運動,設運動時間為t秒.連接PQ.
(1)填空:b= ,c= ;
(2)在點P,Q運動過程中,△APQ可能是直角三角形嗎?請說明理由;
(3)在x軸下方,該二次函數的圖象上是否存在點M,使△PQM是以點P為直角頂點的等腰直角三角形?若存在,請求出運動時間t;若不存在,請說明理由;
(4)如圖②,點N的坐標為(﹣![]() ,0),線段PQ的中點為H,連接NH,當點Q關于直線NH的對稱點Q′恰好落在線段BC上時,請直接寫出點Q′的坐標.
,0),線段PQ的中點為H,連接NH,當點Q關于直線NH的對稱點Q′恰好落在線段BC上時,請直接寫出點Q′的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com