
【題目】如圖1,已知開口向下的拋物線y1=ax2﹣2ax+1過點A(m,1),與y軸交于點C,頂點為B,將拋物線y1繞點C旋轉180°后得到拋物線y2 , 點A,B的對應點分別為點D,E.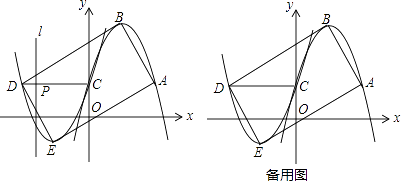
(1)直接寫出點A,C,D的坐標;
(2)當四邊形ABCD是矩形時,求a的值及拋物線y2的解析式;
(3)在(2)的條件下,連接DC,線段DC上的動點P從點D出發,以每秒1個單位長度的速度運動到點C停止,在點P運動的過程中,過點P作直線l⊥x軸,將矩形ABDE沿直線l折疊,設矩形折疊后相互重合部分面積為S平方單位,點P的運動時間為t秒,求S與t的函數關系.
【答案】
(1)
解:由題意得:
將A(m,1)代入y1=ax2﹣2ax+1得:am2﹣2am+1=1,
解得:m1=2,m2=0(舍),
∴A(2,1)、C(0,1)、D(﹣2,1);
(2)
解:如圖1,
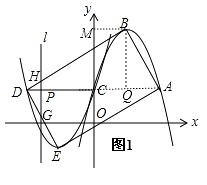
由(1)知:B(1,1﹣a),過點B作BM⊥y軸,
若四邊形ABDE為矩形,則BC=CD,
∴BM2+CM2=BC2=CD2,
∴12+(﹣a)2=22,
∴a= ![]()
![]() ,
,
∵y1拋物線開口向下,
∴a=﹣ ![]() ,
,
∵y2由y1繞點C旋轉180°得到,則頂點E(﹣1,1﹣ ![]() ),
),
∴設y2=a(x+1)2+1﹣ ![]() ,則a=
,則a= ![]() ,
,
∴y2= ![]() x2+2
x2+2 ![]() x+1;
x+1;
(3)
解:如圖2,
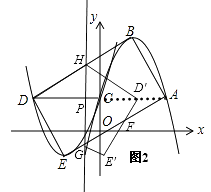
當0≤t≤1時,則DP=t,構建直角△BQD,
得BQ= ![]() ,DQ=3,則BD=2
,DQ=3,則BD=2 ![]() ,
,
∴∠BDQ=30°,
∴PH= ![]() t,PG=
t,PG= ![]() t,
t,
∴S= ![]() (PE+PF)×DP=
(PE+PF)×DP= ![]() t2,
t2,
如圖2,當1<t≤2時,EG=E′G= ![]() (t﹣1),E′F=2(t﹣1),
(t﹣1),E′F=2(t﹣1),
S不重合= ![]() (t﹣1)2,
(t﹣1)2,
S=S1+S2﹣S不重合= ![]() +
+ ![]() (t﹣1)﹣
(t﹣1)﹣ ![]() (t﹣1)2,
(t﹣1)2,
=﹣ ![]()
綜上所述:S= ![]() t2(0≤t≤1)或S=﹣
t2(0≤t≤1)或S=﹣ ![]() (1<t≤2).
(1<t≤2).
【解析】本題考查了二次函數的性質,旋轉的性質和矩形對角線的性質,以及三角函數及特殊角的應用,綜合性較強;善于從已知中挖掘隱藏條件是本題的關鍵:如此題可以計算矩形的邊長及對角線與邊的夾角,得出30°,以此為突破口,將需要的邊長用t表示,得出函數關系式;另外本題還運用了分類討論的思想,這在二次函數中運用較多,應熟練掌握.(1)直接將點A的坐標代入y1=ax2﹣2ax+1得出m的值,因為由圖象可知點A在第一象限,所以m≠0,則m=2,寫出A,C的坐標,點D與點A關于點C對稱,由此寫出點D的坐標;(2)根據頂點坐標公式得出拋物線y1的頂點B的坐標,再由矩形對角線相等且平分得:BC=CD,在直角△BMC中,由勾股定理列方程求出a的值得出拋物線y1的解析式,由旋轉的性質得出拋物線y2的解析式;(3)分兩種情況討論:①當0≤t≤1時,S=S△GHD=S△PDH+S△PDG , 作輔助線構建直角三角形,求出PG和PH,利用面積公式計算;②當1<t≤2時,S=S直角三角形+S矩形﹣S不重合 , 這里不重合的圖形就是△GE′F,利用30°角和60°角的直角三角形的性質進行計算得出結論.
【考點精析】通過靈活運用二次函數的性質和矩形的性質,掌握增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小;矩形的四個角都是直角,矩形的對角線相等即可以解答此題.


 走進文言文系列答案
走進文言文系列答案科目:初中數學 來源: 題型:
【題目】如圖,MN,EF是兩面互相平行的鏡面,一束光線AB照射到鏡面MN上,反射光線為BC,則∠1=∠2.
(1)用尺規作圖作出鏡面BC經鏡面EF反射后的反射光線CD;
(2)試判斷AB與CD的位置關系;
(3)你是如何思考的?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線y=﹣ ![]() x+3與坐標軸分別交于點A,B,點P在拋物線y=﹣
x+3與坐標軸分別交于點A,B,點P在拋物線y=﹣ ![]() (x﹣
(x﹣ ![]() )2+4上,能使△ABP為等腰三角形的點P的個數有( )
)2+4上,能使△ABP為等腰三角形的點P的個數有( )
A.3個
B.4個
C.5個
D.6個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①所示是一個長為2m,寬為2n的長方形,沿圖中虛線用剪刀均分成四個小長方形,然后按圖②的方式拼成一個正方形.
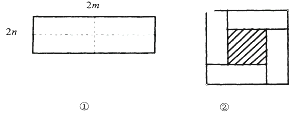
(1)你認為圖②中的陰影部分的正方形的邊長等于_________________.
(2)請用兩種不同的方法列代數式表示圖②中陰影部分的面積.
方法①_________________________________________________________.
方法②_________________________________________________________.
(3)觀察圖②,你能寫出(m+n)2,(m-n)2,mn這三個代數式間的等量關系嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個自行車隊進行訓練,訓練時所有隊員都以相同的速度前進,突然,1號隊員以每小時比其他隊員快10千米的速度獨自行進,行進了10千米后掉轉車頭,速度不變往回騎,直到與其他的隊員會合.從1號隊員離隊開始到與其他隊員重新會合,經過了15分鐘.
(1)其他隊員的行進速度是多少?
(2)1號隊員從離隊開始到與隊員重新會合這個過程中,經過多長時間與其他隊員相距1千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市對進貨價為10元/千克的某種蘋果的銷售情況進行統計,發現每天銷售量y(千克)與銷售價x(元/千克)存在一次函數關系,如圖所示. 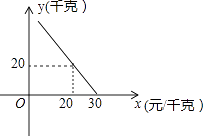
(1)求y關于x的函數關系式(不要求寫出x的取值范圍);
(2)應怎樣確定銷售價,使該品種蘋果的每天銷售利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,CA=CB,∠ACB=90°,AB=2,點D為AB的中點,以點D為圓心作圓心角為90°的扇形DEF,點C恰在弧EF上,則圖中陰影部分的面積為( )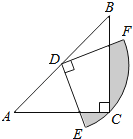
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
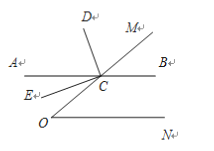
【題目】已知:如圖,點C在∠MON的一邊OM上,過點C的直線AB∥ON,CD平分∠ACM,CE⊥CD.
(1)若∠O=50°,求∠BCD的度數;
(2)求證:CE平分∠OCA;
(3)當∠O為多少度時,CA分∠OCD成1:2兩部分,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com