
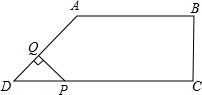
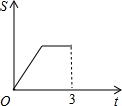
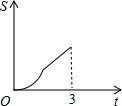
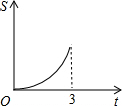
 在直角梯形ABCD中,AB∥CD,BC⊥DC于點C,AB=2,CD=3,∠D=45°,動點P從D點出發,沿DC以每秒1個單位長度的速度移動,到C點停止.過P點作PQ垂直于直 線 AD,垂足為Q.設P點移動的時間為t秒,△DPQ與直角梯形ABCD重疊部分的面積為S,下列圖象中,能表示S與t的函數關系的圖象大致是
在直角梯形ABCD中,AB∥CD,BC⊥DC于點C,AB=2,CD=3,∠D=45°,動點P從D點出發,沿DC以每秒1個單位長度的速度移動,到C點停止.過P點作PQ垂直于直 線 AD,垂足為Q.設P點移動的時間為t秒,△DPQ與直角梯形ABCD重疊部分的面積為S,下列圖象中,能表示S與t的函數關系的圖象大致是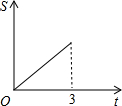
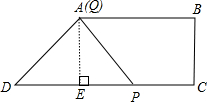 解:過點A作AE⊥CD于E,
解:過點A作AE⊥CD于E, ,
, 時,
時, t,
t,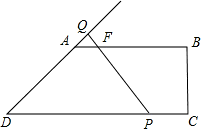
 t•
t• t=
t= t2;
t2; <t≤3時,
<t≤3時, t,AQ=FQ=
t,AQ=FQ= t-
t- ,
, t2-(
t2-( t-
t- )2=2t-2.
)2=2t-2.

 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
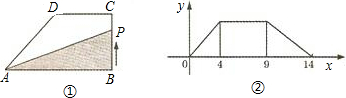
 如圖,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿過點D的直線折疊,使點A剛好落在BC邊上,則此時折痕的長為
如圖,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿過點D的直線折疊,使點A剛好落在BC邊上,則此時折痕的長為5
| ||
| 2 |
| 5 |
5
| ||
| 2 |
| 5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com