【題目】如圖，在菱形ABCD中，AB＝6，∠ABC＝60°，M為AD中點，P為對角線BD上一動點，連接PA和PM，則PA＋PM的最小值是( )
A.3B.2
C.3D.6
【答案】C
【解析】
首先連接AC，交BD于點O，連接CM，則CM與BD交于點P，此時PA+PM的值最小，由在菱形ABCD中，AB=6，∠ABC=60°，易得△ACD是等邊三角形，BD垂直平分AC，繼而可得CM⊥AD，則可求得CM的值，繼而求得PA+PM的最小值．
解：連接AC，交BD于點O，連接CM，則CM與BD交于點P，此時PA+PM的值最小，
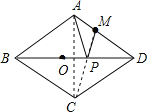
∵在菱形ABCD中，AB=6，∠ABC=60°，
∴∠ADC=∠ABC=60°，AD=CD=6，BD垂直平分AC，
∴△ACD是等邊三角形，PA=PC，
∵M為AD中點，
∴DM=
AD=3，CM⊥AD，
∴CM=
=3
，
∴PA+PM=PC+PM=CM=3．
故選：C．
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】下圖的轉盤被劃分成六個相同大小的扇形，并分別標上1，2，3，4，5，6這六個數字，指針停在每個扇形的可能性相等。四位同學各自發表了下述見解：
甲：如果指針前三次都停在了3號扇形，下次就一定不會停在3號扇形；
乙：只要指針連續轉六次，一定會有一次停在6號扇形；
丙：指針停在奇數號扇形的概率與停在偶數號扇形的概率相等；
丁：運氣好的時候，只要在轉動前默默想好讓指針停在6號扇形，指針停在6號扇形的可能性就會加大。
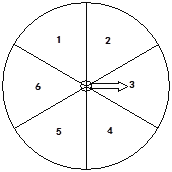
其中，你認為正確的見解有（ ）
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，一列快車從甲地駛往乙地，一列慢車從乙地駛往甲地，兩車同時出發，設慢車行駛的時間為
，兩車之間的距離為
，圖中的折線表示
與
之間的關系，下列說法中正確的個數為（ ）.①甲乙兩地相距
；②
段表示慢車先加速后減速最后到達甲地；③快車的速度為
；④慢車的速度為
；⑤快車到達乙地
后，慢車到達甲地。
A. 
個B. 
個C. 
個D. 
個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】正方形網格中（網格中的每個小正方形邊長是1），△ABC的頂點均在格點上，請在所給的直角坐標系中解答下列問題：
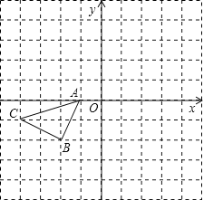
（1）作出△ABC繞點A逆時針旋轉90°的△AB1C1．
（2）作出△AB1C1關于原點O成中心對稱的△A1B2C2．
（3）請直接寫出以A1、B2、C2為頂點的平行四邊形的第四個頂點D的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校為了解2014年八年級學生課外書籍借閱情況，從中隨機抽取了50名學生課外書籍借閱情況，將統計結果列出如下的表格，并繪制成如圖所示的扇形統計圖，其中科普類冊數占這50名學生借閱總冊數的40%．
類別 | 科普類 | 教輔類 | 文藝類 | 其他 |
冊數（本） | 168 | 105 | m | 32 |
（1）表格中字母m的值等于 ；
（2）扇形統計圖中“教輔類”所對應的圓心角α的度數為 °；
（3）該校2014年八年級有600名學生，請你估計該年級學生共借閱教輔類書籍約多少本？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】修正后的《水污染防治法》于2018年1月1日起施行，某企業為了提高污水處理的能力，決定購買10臺污水處理設備，現有
兩種型號的設備，其中每臺的價格、月處理污水量如下表：
|
| |
價格（萬元/臺） | 12 | 10 |
處理污水量（噸/月） | 240 | 200 |
經預算，該企業購買設備的資金不高于105萬元.
（1）請你設計該企業可能的購買方案；
（2）若企業每月產生的污水量為2040噸，為了節約資金，應選擇哪種購買方案？請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為改善生態環境，促進國土綠化，某市甲、乙兩支志愿者隊伍分別參加了兩地的植樹活動．
（1）甲隊在
地植樹，如果每人種
棵，還剩下
棵樹苗；如果每人種
棵，則缺少
棵樹苗．求甲隊志愿者的人數和地需種植的樹苗數．
（2）乙隊在
地植樹，原計劃植樹
棵，由于另有新加入的志愿者共同參與植樹，每日比原計劃多種
，結果提前
天完成任務．問原計劃每天植樹多少棵？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，一次函數y=2x-5的圖象經過正方形OABC的頂點A和C，則正方形OABC的面積為( )
A.9B.10C.12D.13
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
