Question

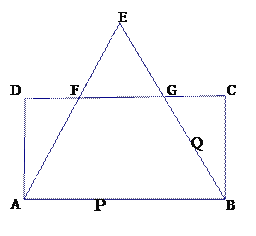
【題目】矩形中， ，以為邊向上作正, 、分別交于、， ，兩動點、運動速度分別為4、 ().

（1）的長為 ；

（2）若點從出發沿線段向運動，同時點從出發沿線段向點運動，設運動時間為，在運動過程中，以、、為頂點的三角形和以、、為頂點的三角形全等，求的運動速度；

（3）若點以（2）中的速度從點出發，同時點以原來的速度從點出發，逆時針沿四邊形運動．問、會不會相遇？若不相遇，說明理由．若相遇，請求出經過多長時間、第一次在四邊形的何處相遇？

Answer 1

【答案】(1)AF=10cm；（2）或4cm\s；（3）5圈又運動了22cm后在BG邊距點B 4cm處與點Q相遇.

【解析】試題分析：（1）先由△ABE是等邊三角形，DF=5cm，求出FG的長，再由△EFG∽△EAB,對應邊成比例求出AF的長；（2）先表示出AP、PB長，再由△AFP≌△BQP或△AFP≌△BPQ，

對應邊相等列出方程解即可得到答案；（3）當Q的速度為V=4cm\s時，點P的速度也為4cm\s ，兩點同向同速， 此時P，Q不會相遇；當Q的速度為V=時設經過xsP、第一次相遇，根據題意得： ，即可得到經過63sP、第一次相遇.

試題解析：（1）∵△ABE是等邊三角形，DF=5cm,

∴CG=5cm,∴FG=18-5-5=8cm,

∵FG∥AB,

△EFG∽△EAB,

∴,即，

∴AF=10cm

(2)又題意得：AP=4t，PB=18-4t

①當△AFP≌△BPQ時，PB=AF 即：18-4t=10 ∴t=2s，此時：AP=4t=8cm=BQ，2V=8 ∴V=4cm\s

②當△AFP≌△BQP時，AF=BQ ，AP=PB，即：4t=18-4t

解得：t= ， 解得：V=

(3)解：①當Q的速度為V=4cm\s時，因為點P的速度也為4cm\s ∴P，Q不會相遇

②當點Q的速度為V=時，∵＞4cm\s

∴點Q能追上點P

設：追上的時間為xs.又∵P,Q沿逆時針運動，Q 、P距離為28cm，

根據題意得： 解得：x=63s

又∵P的速度為4cm\s，∴P運動63s共走了：

而P從A出發逆時針，沿四邊形ABGF的邊運動，轉一圈為46cm

∵46×5+22=252

∴P在沿四邊形ABGF的邊逆時針運動了5圈又運動了22cm后在BG邊距點B 4cm處與點Q相遇（或距離點G6cm處與點Q相遇）