
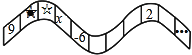
【題目】如圖,從左邊第一個格子開始向右數,在每個小格子中都填入一個整數,使得其中任意三個相鄰格子中所填整數之和都相等.
(![]() )可求得
)可求得![]() __________,第
__________,第![]() 個格子中的數為__________.
個格子中的數為__________.
(![]() )判斷:前
)判斷:前![]() 個格子中所填整數之和是否可能為
個格子中所填整數之和是否可能為![]() ?若能,求出
?若能,求出![]() 的值,若不能,請說明理由.
的值,若不能,請說明理由.
(![]() )若取前
)若取前![]() 格子中的任意兩個數記作
格子中的任意兩個數記作![]() 、
、![]() ,且
,且![]() ,那么所有的
,那么所有的![]() 的和可以通過計算
的和可以通過計算![]() 得到,其結果為__________;若
得到,其結果為__________;若![]() 、
、![]() 為前
為前![]() 格子中的任意兩個數記作
格子中的任意兩個數記作![]() 、
、![]() ,且
,且![]() ,則所有的
,則所有的![]() 的和為__________.
的和為__________.
【答案】(![]() )
)![]() ;
; ![]() (
(![]() )能,
)能, ![]() (
(![]() )
)![]()
【解析】試題分析:(1)根據三個相鄰格子的整數的和相等列式求出x的值,再根據第9個數是2可得☆=2,然后找出格子中的數是每3個為一個循環組依次循環,再用2017除以3,根據余數的情況確定與第幾個數相同即可得解;
(2)可先計算出這三個數的和,再按照規律計算.
(3)由于是三個數重復出現,因此可用前三個數的重復多次計算出結果.
試題解析:解:(![]() )∵任意三個相鄰格子中所填的整數之和都相等,∴表格中從左向右三個數字一個循環,∴
)∵任意三個相鄰格子中所填的整數之和都相等,∴表格中從左向右三個數字一個循環,∴![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,∴第
,∴第![]() 個格子中填的數是
個格子中填的數是![]() .
.
(![]() )能,
)能, ![]() .∵
.∵![]() ;
; ![]() ;用
;用![]() .
.
當前![]() 個格子中的數的和是
個格子中的數的和是![]() ,∴多一個格子數的和是
,∴多一個格子數的和是![]() ,再多一個格子的數的和是
,再多一個格子的數的和是![]() 符合題意,所以
符合題意,所以![]() 的值是
的值是![]() .
.
(![]() )∵取前
)∵取前![]() 格子中的任意兩個數,記作
格子中的任意兩個數,記作![]() ,
, ![]() ,且
,且![]() ,∴所有
,∴所有![]() 的和為:
的和為: ![]() .∵由于三個數重復出現,那么前
.∵由于三個數重復出現,那么前![]() 格子中這三個數
格子中這三個數![]() 出現了
出現了![]() 次,
次, ![]() 和
和![]() 各出現了
各出現了![]() 次,∴代入式子可得
次,∴代入式子可得![]() ,
,
答: ![]() 結果為
結果為![]() ,所有的
,所有的![]() 的和為
的和為![]() .
.


科目:初中數學 來源: 題型:
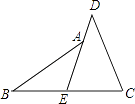
【題目】閱讀下面的題目及分析過程,并按要求進行證明. 已知:如圖,E是BC的中點,點A在DE上,且∠BAE=∠CDE.
求證:AB=CD.
分析:證明兩條線段相等,常用的一般方法是應用全等三角形或等腰三角形的判定和性質,觀察本題中要證明的兩條線段,它們不在同一個三角形中,且它們分別所在的兩個三角形也不全等.因此,要證AB=CD,必須添加適當的輔助線,構造全等三角形或等腰三角形.
現給出如下三種添加輔助線的方法,請任意選擇其中一種,對原題進行證明.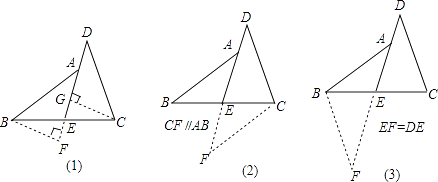
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列幾個命題:①相等的角是對頂角;②同位角都相等;③三個角相等的三角形是等邊三角形;④兩直線平行,內錯角相等;⑤若a2=b2,則a=b.其中真命題的個數有( )
A. 0個 B. 1個 C. 2個 D. 3個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上三點A,O,B表示的數分別為6,0,-4,動點P從A出發,以每秒6個單位的速度沿數軸向左勻速運動.
(1)當點P到點A的距離與點P到點B的距離相等時,點P在數軸上表示的數是 ;
(2)另一動點R從B出發,以每秒4個單位的速度沿數軸向左勻速運動,若點P、R同時出發,問點P運動多少時間追上點R?
(3)若M為AP的中點,N為PB的中點,點P在運動過程中,線段MN的長度是否發生變化?若發生變化,請你說明理由;若不變,請你畫出圖形,并求出線段MN的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義新運算“※”,規則:a※b=ab﹣a﹣b,如1※2=1×2﹣1﹣2=﹣1,若x2+x﹣1=0的兩根為x1 , x2 , 則x1※x2= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】到三角形三個頂點距離相等的點是( )
A. 三角形三條角平分線的交點 B. 三角形的三條中線的交點
C. 三角形三邊垂直平分線的交點 D. 三角形三條高線的交點
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com