
對于任意兩個二次函:y1=a1x2+b1x+c1,y2=a2x2+b2x+c2,(a1a2≠0),當|a1|=|a2|時,我們稱這兩個二次函數的圖象為全等拋物線.
現有△ABM,A(- l,O),B(1,0).記過三點的二次函數拋物線為-C□□□?摗酢酢鯏中填寫相應三個點的字母)

(1)若已知M(0,1),△ABM≌△ABN(10-l).請通過計算判斷CABM與CABN是否為全等拋物線;
(2)在圖10-2中,以A、B、M三點為頂點,畫出平行四邊形.
①若已知 M(0, л),求拋物線CABM的解析式,并直接寫出所有過平行四邊形中三個頂點且能與CABM全等的拋物線解析式.
②若已知M(m,n),當m,n滿足什么條件時,存在拋物線CABM?根據以上的探究結果,判斷是否存在過平行四邊形中三個頂點且能與CABM全等的拋物線,若存在,請列出所有滿足條件的拋物線-C□□□敚蝗舨淮嬖冢?胨得骼磧桑?/P>
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
| 2013 |
| x |
| 1 |
| 5 |
| 4 |
| 5 |
| 7 |
| 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
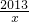 是閉區間[1,2013]上的“閉函數”嗎?請判斷并說明理由;
是閉區間[1,2013]上的“閉函數”嗎?請判斷并說明理由; x2-
x2- x-
x- 是閉區間[a,b]上的“閉函數”,求實數a,b的值.
是閉區間[a,b]上的“閉函數”,求實數a,b的值.查看答案和解析>>
科目:初中數學 來源:長沙 題型:解答題
| 2013 |
| x |
| 1 |
| 5 |
| 4 |
| 5 |
| 7 |
| 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:
設![]() 是任意兩個不等實數,我們規定:滿足不等式
是任意兩個不等實數,我們規定:滿足不等式![]() 的實數
的實數![]() 的所有取值的全體叫做閉區間,表示為
的所有取值的全體叫做閉區間,表示為![]() .對于一個函數,如果它的自變量
.對于一個函數,如果它的自變量![]() 與函數值
與函數值![]() 滿足:當
滿足:當![]() 時,有
時,有![]() ,我們就
,我們就![]() 稱此函數是閉區間
稱此函數是閉區間![]() 上的“閉函數”.
上的“閉函數”.
(1)反比例函數![]() 是閉區間
是閉區間![]() 上的“閉函數”嗎?請判斷并說明理由;
上的“閉函數”嗎?請判斷并說明理由;
(2)若一次函數![]() 是閉區間
是閉區間![]() 上的“閉函數”,求此函數的解析式;
上的“閉函數”,求此函數的解析式;
(3)若二次函數![]() 是閉區間
是閉區間![]() 上的“閉函數”,求實數
上的“閉函數”,求實數![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com