
在直角坐標系中,點A是拋物線y=x2在第二象限上的點,連接OA,過點O作OB⊥OA,交拋物線于點B,以OA、OB為邊構造矩形AOBC.
(1)如圖1,當點A的橫坐標為 時,矩形AOBC是正方形;
(2)如圖2,當點A的橫坐標為 時,
時,
①求點B的坐標;
②將拋物線y=x2作關于x軸的軸對稱變換得到拋物線y=-x2,試判斷拋物線y=-x2經過平移交換后,能否經過A,B,C三點?如果可以,說出變換的過程;如果不可以,請說明理由.
解:(1) -1。
(2) ①過點A作AE⊥x軸于點E,過點B作BF⊥x軸于點F,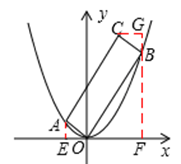
當x=-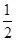 時,y=(-
時,y=(-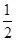 )2=
)2=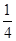 ,
,
即OE=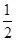 ,AE=
,AE=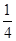 。
。
∵∠AOE+∠BOF=180°-90°=90°,21世
∠AOE+∠EAO=90°,
∴∠EAO=∠BOF。
又∵∠AEO=∠BFO=90°,∴△AEO∽△OFB。
∴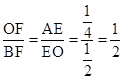 。
。
設OF=t,則BF=2t,∴t2=2t,解得:t1=0(舍去),t2=2。
∴點B(2,4)。
②過點C作CG⊥BF于點G,
∵∠AOE+∠EAO=90°,∠FBO+∠CBG=90°,∠EOA=∠FBO,
∴∠EAO=∠CBG。
在△AEO和△BGC中,∠AEO=∠G=900,∠EAO=∠CBG,AO=BC,
∴△AEO≌△BGC(AAS)。∴CG=OE=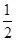 ,BG=AE=
,BG=AE=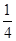 。
。
∴xc=2- ,yc=4+
,yc=4+ 。∴點C(
。∴點C(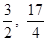 )。
)。
設過A(-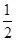 ,
,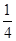 )、B(2,4)兩點的拋物線解析式為y=-x2+bx+c,由題意得,
)、B(2,4)兩點的拋物線解析式為y=-x2+bx+c,由題意得,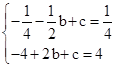 ,得
,得 。
。
∴經過A、B兩點的拋物線解析式為y=-x2+3x+2。
∵當x=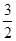 時,y=-(
時,y=-(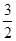 )2+3×
)2+3×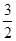 +2=
+2=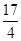 ,∴點C也在此拋物線上。
,∴點C也在此拋物線上。
∴經過A、B、C三點的拋物線解析式為y=-x2+3x+2=-(x-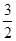 )2+
)2+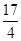 。
。
平移方案:先將拋物線y=-x2向右平移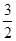 個單位,再向上平移
個單位,再向上平移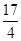 個單位得到拋物線
個單位得到拋物線
y=-(x-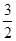 )2+
)2+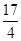 。
。
解析


科目:初中數學 來源: 題型:
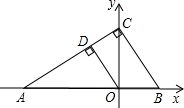 C作CB⊥AC,交x軸于B.
C作CB⊥AC,交x軸于B.查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com