
【題目】如圖,在平面直角坐標系中,拋物線y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C,對稱軸與x軸交于點D,點E(4,n)在拋物線上.
與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C,對稱軸與x軸交于點D,點E(4,n)在拋物線上.

(1)求直線AE的解析式;
(2)點P為直線CE下方拋物線上的一點,連接PC,PE.當△PCE的面積最大時,求P點坐標?
(3)點G是線段CE的中點,將拋物線y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 沿x軸正方向平移得到新拋物線y′,y′經過點D,y′的頂點為點F.在新拋物線y′的對稱軸上,是否存在點Q,使得△FGQ為等腰三角形?若存在,直接寫出點Q的坐標;若不存在,請說明理由.
沿x軸正方向平移得到新拋物線y′,y′經過點D,y′的頂點為點F.在新拋物線y′的對稱軸上,是否存在點Q,使得△FGQ為等腰三角形?若存在,直接寫出點Q的坐標;若不存在,請說明理由.
【答案】(1) y= ![]() x+
x+ ![]() (2) P(2,﹣
(2) P(2,﹣![]() )(3) (3,
)(3) (3,![]() )或(3,
)或(3,![]() )或(3,2
)或(3,2![]() )或(3,﹣
)或(3,﹣![]() )
)
【解析】試題分析:(1)拋物線的解析式可變形為y=![]() (x+1)(x-3),從而可得到點A和點B的坐標,然后再求得點E的坐標,設直線AE的解析式為y=kx+b,將點A和點E的坐標代入求得k和b的值,從而得到AE的解析式;
(x+1)(x-3),從而可得到點A和點B的坐標,然后再求得點E的坐標,設直線AE的解析式為y=kx+b,將點A和點E的坐標代入求得k和b的值,從而得到AE的解析式;
(2)設直線CE的解析式為y=mx-![]() ,將點E的坐標代入即可確定直線CE的解析式,過點P作PF∥y軸,交CE與點F,設點P的坐標為(x,
,將點E的坐標代入即可確定直線CE的解析式,過點P作PF∥y軸,交CE與點F,設點P的坐標為(x,![]() x2
x2![]() x
x![]() ),求出PF的值,表示出△EPC的面積,再利用二次函數的性質可求得x的值,從而得到點P的坐標;
),求出PF的值,表示出△EPC的面積,再利用二次函數的性質可求得x的值,從而得到點P的坐標;
(3)由平移后的拋物線經過點D,可得到點F的坐標,利用中點坐標公式可求得點G的坐標,然后分為FG=FQ、GF=GQ,QG=QF三種情況求解即可.
解:(1)∵y=![]() x2-
x2-![]() x-
x-![]() ,
,
∴y=![]() (x+1)(x-3).
(x+1)(x-3).
∴A(-1,0),B(3,0).
當x=4時,y=![]() .
.
∴E(4,![]() ),
),
設直線AE的解析式為y=kx+b,將點A和點E的坐標代入得:
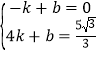 ,
,
計算得出:k=![]() ,b=
,b=![]() ,
,
∴直線AE的解析式為y=![]() x+
x+![]()
(2)設直線CE的解析式為y=mx-![]() ,將點E的坐標代入得4m-
,將點E的坐標代入得4m-![]() =
=![]() ,計算出m=
,計算出m=![]() .
.
∴直線CE的解析式為y=![]() x-
x-![]() .
.
過點P作PF∥y軸,交CE與點F,如圖①所示.
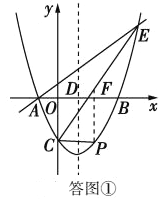
設點P的坐標為(x,![]() x2
x2![]() x
x![]() ),則點F(x,
),則點F(x,![]() x
x![]() ),
),
則FP=(![]() x
x![]() )-(
)-(![]() x2
x2![]() x
x![]() )=-
)=-![]() x2+
x2+![]() x,
x,
∴△EPC的面積=![]() ×(-
×(-![]() x2+
x2+![]() x)×4=-
x)×4=-![]() x2+
x2+![]() x.
x.
∴當x=2時,△EPC的面積最大.
∴P(2,-![]() ).
).
(3)如圖②所示:
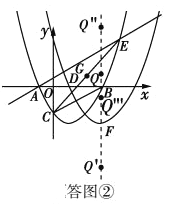
∵y′經過點D,y′的頂點為點F,
∴點F(3,-![]() ).
).
∵點G為CE的中點,
∴G(2,![]() ).
).
∴FG=![]() ,.
,.
∴當FG=FQ時,點Q(3,![]() ),Q′(3,
),Q′(3,![]() ).
).
當GF=GQ時,點F與點Q″關于y=![]() 對稱,
對稱,
∴點Q″(3,2![]() ).
).
當QG=QF時,設點Q1的的坐標為(3,a).
由兩點間的距離公式可以知道:a+![]() =
=![]() ,計算得出:a=-
,計算得出:a=-![]() .
.
∴點Q1的坐標為(3,-![]() ).
).
綜上所述,點Q的坐標為(3,![]() )或(3,
)或(3,![]() )或(3,2
)或(3,2![]() )或(3,-
)或(3,-![]() ).
).


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:初中數學 來源: 題型:
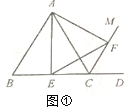
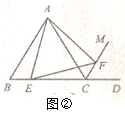
【題目】【感知】如圖①,△ABC是等邊三角形,CM是外角∠ACD的平分線,E是邊BC中點,在CM上截取CF=BE,連接AE、EF、AF.易證:△AEF是等邊三角形(不需要證明).
【探究】如圖②,△ABC是等邊三角形,CM是外角∠ACD的平分線,E是邊BC上一點(不與點B、C重合),在CM上截取CF=BE,連接AE、EF、AF.求證:△AEF是等邊三角形.
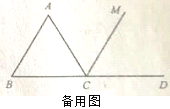
【應用】將圖②中的“E是邊BC上一點”改為“E是邊BC延長線上一點”,其他條件不變.當四邊形ACEF是軸對稱圖形,且AB=2時,請借助備用圖,直接寫出四邊形ACEF的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】江蘇衛視《最強大腦》曾播出一期“辨臉識人”節目,參賽選手以家庭為單位,每組家庭由爸爸媽媽和寶寶3人組成,爸爸、媽媽和寶寶分散在三塊區域,選手需在寶寶中選一個寶寶,然后分別在爸爸區域和媽媽區域中正確找出這個寶寶的父母,不考慮其他因素,僅從數學角度思考,已知在本期比賽中有A、B、C三組家庭進行比賽.
(1)若機器人智能小度選擇A組家庭的寶寶,求小度在媽媽區域中正確找出其媽媽的概率;
(2)如果任選一個寶寶(假如選A組家庭),通過列表或樹狀圖的方法,求機器人智能小度至少正確找對寶寶父母其中一人的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有兩桶水,甲桶裝有![]() 升水,乙桶中的水比甲桶中的水多3升.現將甲桶中倒一半到乙桶中,然后再將此時乙桶中總水量的
升水,乙桶中的水比甲桶中的水多3升.現將甲桶中倒一半到乙桶中,然后再將此時乙桶中總水量的![]() 倒給甲桶,假定桶足夠大,水不會溢岀.我們將上述兩個步驟稱為一次操作,進行重復操作,則( )
倒給甲桶,假定桶足夠大,水不會溢岀.我們將上述兩個步驟稱為一次操作,進行重復操作,則( )
A. 每操作一次,甲桶中的水量都會減小,最后甲桶中的水會全部倒入乙桶
B. 每操作一次,甲桶中的水量都會減小,但永遠倒不完
C. 每操作一次,甲桶中的水量都會增加,反復操作,最后甲桶中的水會比乙桶多
D. 每操作一次,甲桶中的水量都會增加,但永遠比乙桶中的水量要少
查看答案和解析>>
科目:初中數學 來源: 題型:
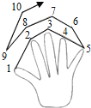
【題目】 從大拇指開始,按照大拇指→食指→中指→無名指→小指→無名指→中指→食指→大拇指→食指……的順序,依次數整數1、2、3、4、5,6、7、…,當數到4019時對應的手指為_____;當第n次數到無名指時,數到的數是_____(用含n的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD與四邊形BEFG都是正方形,設AB=a,DE=b(a>b).

(1)寫出AG的長度(用含字母a、b的代數式表示);
(2)觀察圖形,試用不同的方法表示圖形中陰影部分的面積,你能獲得相應的一個因式分解公式嗎?請將這個公式寫出來;
(3)如果正方形ABCD的邊長比正方形DEFG的邊長多16cm,它們的面積相差960cm2.試利用⑵中的公式,求a、b的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】嘉淇準備完成題目:化簡:![]() ,發現系數“
,發現系數“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,請你化簡:(3x2+6x+8)–(6x+5x2+2);
”猜成3,請你化簡:(3x2+6x+8)–(6x+5x2+2);
(2)他媽媽說:“你猜錯了,我看到該題標準答案的結果是常數.”通過計算說明原題中“![]() ”是幾?
”是幾?
查看答案和解析>>
科目:初中數學 來源: 題型:
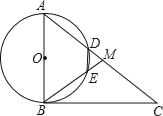
【題目】如圖,在Rt△ABC中,∠ABC=90°,點M是AC的中點,以AB為直徑作⊙O分別交AC,BM于點D,E.連結DE,使四邊形DEBA為⊙O的內接四邊形.
(1)求證:∠A=∠ABM=∠MDE;
(2)若AB=6,當AD=2DM時,求DE的長度;
(3)連接OD,OE,當∠A的度數為60°時,求證:四邊形ODME是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解學校開展“孝敬父母,從家務勞動做起”活動的實施情況,該校抽取八年級50名學生,調查他們一周(按七天計算)做家務所用時間(單位:小時)得到一組數據,繪制成下表:
時間x(小時) | 劃記 | 人數 | 所占百分比 |
0.5x≤x≤1.0 | 正正 | 14 | 28% |
1.0≤x<1.5 | 正正正 | 15 | 30% |
1.5≤x<2 |
| 7 |
|
2≤x<2.5 |
| 4 | 8% |
2.5≤x<3 | 正 | 5 | 10% |
3≤x<3.5 |
| 3 |
|
3.5≤x<4 |
|
| 4% |
合計 | 50 | 100% |
(1)請填表中未完成的部分;
(2)根據以上信息判斷,每周做家務的時間不超過1.5小時的學生所占的百分比是多少?
(3)針對以上情況,寫出一個20字以內的倡導“孝敬父母,熱愛勞動”的句子.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com