
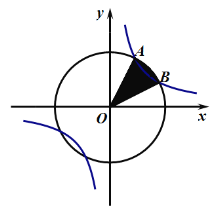
【題目】已知雙曲線![]() 與
與![]() 在第一象限內交于
在第一象限內交于![]() ,
,![]() 兩點,
兩點,![]() ,則扇形
,則扇形![]() 的面積是________.
的面積是________.
【答案】![]()
【解析】
設⊙O的半徑OA=OB=r,連接AB,作直線y=x,與AB交于點C,示、過A作AD⊥y軸于點D,過B作BE⊥x軸于點E,過A作AF⊥OB于點F.由圓與雙曲線的對稱性得△AOD≌△AOC≌△BOC≌△BOE,進而由反比例函數的比例系數的幾何意義得△AOB的面積,再由三角形的面積公式求得圓的半徑,最后由扇形的面積公式求得結果.
設⊙O的半徑OA=OB=r,連接AB,作直線y=x,與AB交于點C,示、過A作AD⊥y軸于點D,過B作BE⊥x軸于點E,過A作AF⊥OB于點F.
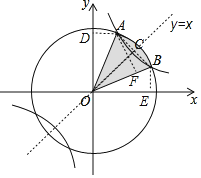
∵⊙O在第一象限關于y=x對稱,![]() (k>0)也關于y=x對稱,
(k>0)也關于y=x對稱,
∴∠AOC=∠BOC,OC⊥AB,∠AOD=∠BOE,
∵∠AOB=45°,
∴∠AOD=∠AOC=∠BOC=∠BOE=22.5°,
由對稱性知,△AOD≌△AOC≌△BOC≌△BOE,
由反比例函數的幾何意義知,![]() ,
,
∴S△AOC=S△BOC=1,
∴S△AOB=1+1=2,
∵∠AOB=45°,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案為:![]() .
.


 同步輕松練習系列答案
同步輕松練習系列答案 課課通課程標準思維方法與能力訓練系列答案
課課通課程標準思維方法與能力訓練系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中拋物線y=(x+1)(x﹣3)與x軸相交于A、B兩點,若在拋物線上有且只有三個不同的點C1、C2、C3,使得△ABC1、△ABC2、△ABC3的面積都等于m,則m的值是( )
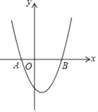
A. 6 B. 8 C. 12 D. 16
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如今很多初中生喜歡購頭飲品飲用,既影響身體健康又給家庭增加不必要的開銷,為此某班數學興趣小組對本班同學一天飲用飲品的情況進行了調查,大致可分為四種:A.白開水,B.瓶裝礦泉水,C.碳酸飲料,D.非碳酸飲料.根據統計結果繪制如下兩個統計圖,根據統計圖提供的信息,解答下列問題
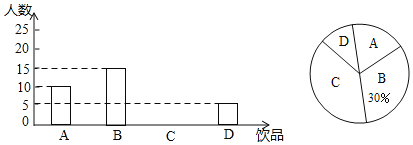
(1)這個班級有多少名同學?并補全條形統計圖;
(2)若該班同學每人每天只飲用一種飲品(每種僅限一瓶,價格如下表),則該班同學每天用于飲品的人均花費是多少元?
飲品名稱 | 白開水 | 瓶裝礦泉水 | 碳酸飲料 | 非碳酸飲料 |
平均價格(元/瓶) | 0 | 2 | 3 | 4 |
(3)為了養成良好的生活習慣,班主任決定在飲用白開水的5名班委干部(其中有兩位班長記為A,B,其余三位記為C,D,E)中隨機抽取2名班委干部作良好習慣監督員,請用列表法或畫樹狀圖的方法求出恰好抽到2名班長的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD邊長為2,E是AB的中點,以E為圓心,線段ED的長為半徑作半圓,交直線AB于點M,N,分別以線段MD,ND為直徑作半圓,則圖中陰影部分的面積為_____________

查看答案和解析>>
科目:初中數學 來源: 題型:
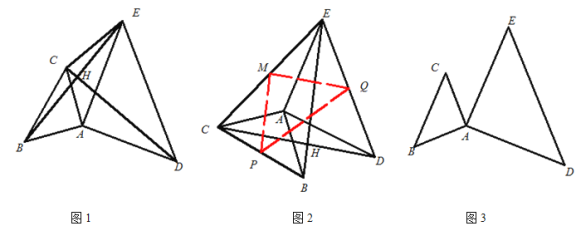
【題目】已知:△ABC和△ADE是兩個不全等的等腰直角三角形,其中AB=AC,AD=AE,
∠BAC=90°,∠DAE=90°.
(1)觀察猜想
如圖1,連接BE、CD交于點H,再連接CE,那么BE和CD的數量關系和位置關系分別是
(2)探究證明
將圖1中的△ABC繞點A逆時針旋轉到圖2的位置時,分別取BC、CE、DE的中點P、M、Q,連接MP、PQ、MQ,請判斷MP和MQ的數量關系和位置關系,并說明理由;
(3)拓展延伸
已知AB=![]() ,AD=4,在(2)的條件下,將△ABC繞點A旅轉的過程中,若∠CAE=45°,請直接寫出此時線段PQ的長.
,AD=4,在(2)的條件下,將△ABC繞點A旅轉的過程中,若∠CAE=45°,請直接寫出此時線段PQ的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的外接圓,過點
的外接圓,過點![]() 作
作![]() 的切線,交
的切線,交![]() 的延長線于點
的延長線于點![]() ,
,![]() 交
交![]() 于點
于點![]() .
.
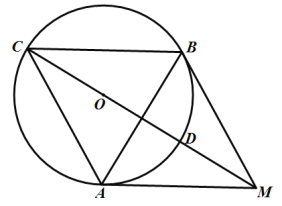
(1)求證:![]() ;
;
(2)填空:
①若![]() ,
,![]() ________;
________;
②連接![]() ,當
,當![]() 的度數為________時,四邊形
的度數為________時,四邊形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
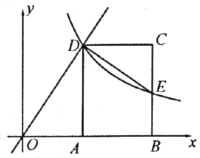
【題目】如圖,在平面直角坐標系中,矩形![]() 的頂點
的頂點![]() ,
,![]() 在
在![]() 軸的正半軸上,頂點
軸的正半軸上,頂點![]() 在直線
在直線![]() 位于第一象限的圖像上,反比例函數
位于第一象限的圖像上,反比例函數![]() 的圖像經過點
的圖像經過點![]() ,交
,交![]() 于點
于點![]() ,
,![]() .
.
(1)如果![]() ,求點
,求點![]() 的坐標;
的坐標;
(2)連接![]() ,當
,當![]() 時,求點
時,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
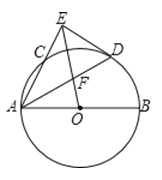
【題目】如圖,AB是⊙O的直徑AC是弦,∠BAC的平分線AD交⊙O于點D,DE⊥AC交AC的延長線于點E,連接OE,OE交AD于點F.
(1)求證:DE是⊙O的切線;
(2)若![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com