
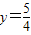 作垂線,垂足為M,連FM(如圖).
作垂線,垂足為M,連FM(如圖).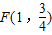 ,求以PM為底邊的等腰三角形PFM的P點的坐標,并證明此時△PFM為正三角形;
,求以PM為底邊的等腰三角形PFM的P點的坐標,并證明此時△PFM為正三角形;
 =1,
=1,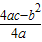 =1,c=0,
=1,c=0, ),
), )2=(m-1)2+(
)2=(m-1)2+( -
- )2
)2 =
= 或-m2+2m-
或-m2+2m- =-
=- ,
, =
= 時,即-4m2+8m-5=0
時,即-4m2+8m-5=0 =-
=- 時,即m2-2m=-
時,即m2-2m=-
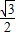 或m=1-
或m=1-
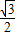 時,P點的坐標為(1+
時,P點的坐標為(1+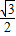 ,
, ),M點的坐標為(1+
),M點的坐標為(1+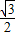 ,
, )
)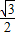 時,P點的坐標為(1-
時,P點的坐標為(1-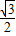 ,
, ),M點的坐標為(1-
),M點的坐標為(1- ,
, ),
),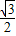 ,
, )或(1-
)或(1- ,
, ).
). 時,即N與F重合時PM=PN恒成立.
時,即N與F重合時PM=PN恒成立.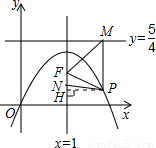
 -y)2=y2-
-y)2=y2- y+
y+ ,
, y+
y+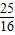 ,
, y+2ty+
y+2ty+ -t2=0,y(2t-
-t2=0,y(2t- )+(
)+( -t2)=0對任意y恒成立.
-t2)=0對任意y恒成立. =0且
=0且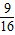 -t2=0,
-t2=0, ,
, 時,PM=PN恒成立.
時,PM=PN恒成立.

科目:初中數學 來源:2010年全國中考數學試題匯編《三角形》(11)(解析版) 題型:解答題
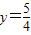 作垂線,垂足為M,連FM(如圖).
作垂線,垂足為M,連FM(如圖).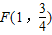 ,求以PM為底邊的等腰三角形PFM的P點的坐標,并證明此時△PFM為正三角形;
,求以PM為底邊的等腰三角形PFM的P點的坐標,并證明此時△PFM為正三角形;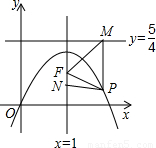
查看答案和解析>>
科目:初中數學 來源:2010年全國中考數學試題匯編《二次函數》(09)(解析版) 題型:解答題
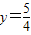 作垂線,垂足為M,連FM(如圖).
作垂線,垂足為M,連FM(如圖). ,求以PM為底邊的等腰三角形PFM的P點的坐標,并證明此時△PFM為正三角形;
,求以PM為底邊的等腰三角形PFM的P點的坐標,并證明此時△PFM為正三角形;
查看答案和解析>>
科目:初中數學 來源:2010年湖北省隨州市中考數學試卷(解析版) 題型:解答題
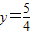 作垂線,垂足為M,連FM(如圖).
作垂線,垂足為M,連FM(如圖).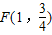 ,求以PM為底邊的等腰三角形PFM的P點的坐標,并證明此時△PFM為正三角形;
,求以PM為底邊的等腰三角形PFM的P點的坐標,并證明此時△PFM為正三角形;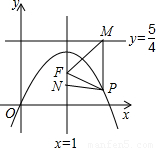
查看答案和解析>>
科目:初中數學 來源:2010年湖北省黃岡市中考數學試卷(解析版) 題型:解答題
 作垂線,垂足為M,連FM(如圖).
作垂線,垂足為M,連FM(如圖).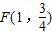 ,求以PM為底邊的等腰三角形PFM的P點的坐標,并證明此時△PFM為正三角形;
,求以PM為底邊的等腰三角形PFM的P點的坐標,并證明此時△PFM為正三角形;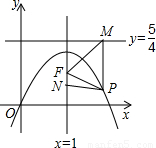
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com