
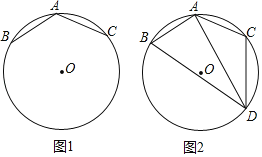
【題目】如圖1,已知A、B、C是⊙O上的三點,AB=AC,∠BAC=120°.
(1)求證:⊙O的半徑R=AB;
(2)如圖2,若點D是∠BAC所對弧上的一動點,連接DA,DB,DC.
①探究DA,DB,DC三者之間的數量關系,并說明理由;
②若AB=3,點C'與C關于AD對稱,連接C'D,點E是C'D的中點,當點D從點B運動到點C時,求點E的運動路徑長.
【答案】(1)見解析;(2)①CD+BD=![]() AD,見解析,②2
AD,見解析,②2![]() π
π
【解析】
(1)連接OA,OB,OC,由“SSS”可證△OAB≌△OAC,可得∠BAO=∠CAO=60°,可證△ABO是等邊三角形,可得結論;
(2)將△ABD繞點A逆時針旋轉120°得到△ACH,過點A作AN⊥CH于N,由旋轉的性質可得BD=CH,AD=AH,∠DAH=120°,∠ABD=∠ACH,可證點D,點C,點H三點共線,由直角三角形的性質可求解;
(3)先確定點E的運動軌跡,利用弧長公式可求解.
證明:(1)如圖1,連接OA,OB,OC,
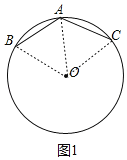
∵AB=AC,OB=OC,OA=OA,
∴△OAB≌△OAC(SSS),
∴∠BAO=∠CAO,
又∵∠BAC=120°,
∴∠OAB=60°=∠OAC,
∴△ABO是等邊三角形,
∴⊙O的半徑R=AB;
(2)CD+BD=![]() AD,
AD,
理由如下:如圖2,將△ABD繞點A逆時針旋轉120°得到△ACH,過點A作AN⊥CH于N,
∴BD=CH,AD=AH,∠DAH=120°,∠ABD=∠ACH,
∵四邊形ABDC是圓內接四邊形,
∴∠ABD+∠ACD=180°,
∴∠ACD+∠ACH=180°,
∴點D,點C,點H三點共線,
∵AD=AH,∠DAH=120°,AN⊥CH,
∴∠AHD=∠ADH=30°,HN=DN=![]() DH,
DH,
∴AD=2AN,DN=![]() AN,
AN,
∴HD=![]() AN=
AN=![]() AD,
AD,
∴CD+CH=CD+BD=![]() AD;
AD;
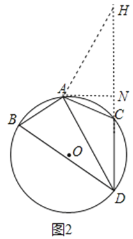
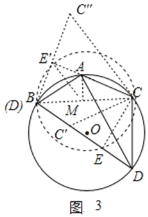
(3)如圖3,連接BC,過點A作AM⊥BC于M,連接CC',CE,
∵AB=AC,∠BAC=120°,AM⊥BC,AB=3,
∴∠ABC=∠ACB=30°,
∴AM=![]() ,BM=
,BM=![]() AM=
AM=![]() ,
,
∵∠ADB=∠ACB=30°,∠ADC=∠ABC=30°,
∴∠ADB=∠ADC,
∴點C關于AD對稱點C'在BD上,
∴CD=C'D,
又∵∠CDC'=60°,
∴△CDC'是等邊三角形,
∵點E是C'D的中點,
∴CE⊥BD,
∴點E在以BC為直徑的圓上,
當點B與點D重合時,
∵E'M=BM=CM,
∴∠MCE'=∠ME'C=30°,
∴∠BME'=60°,
當點D與點C重合時,點E也與點C重合,
∴點E的運動路徑長=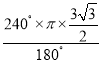 =2
=2![]() π.
π.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:初中數學 來源: 題型:
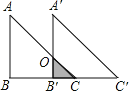
【題目】如圖所示,已知Rt△ABC中,∠B=90°,BC=4,AB=4,現將△ABC沿BC方向平移到△A′B′C′的位置.若平移的距離為3,則△ABC與△A′B′C′重疊部分的陰影面積為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對垃圾進行分類投放,能提高垃圾處理和再利用的效率,減少污染,保護環境.為了檢查垃圾分類的落實情況,某居委會成立了甲、乙兩個檢查組,采取隨機抽查的方式分別對轄區內的A,B,C,D四個小區進行檢查,并且每個小區不重復檢查.
(1)甲組抽到A小區的概率是多少;
(2)請用列表或畫樹狀圖的方法求甲組抽到A小區,同時乙組抽到C小區的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】央視熱播節目“朗讀者”激發了學生的閱讀興趣.某校為滿足學生的閱讀需求,欲購進一批學生喜歡的圖書,學校組織學生會成員隨機抽取部分學生進行問卷調查,被調查學生須從“文史類、社科類、小說類、生活類”中選擇自己喜歡的一類,根據調查結果繪制了統計圖(未完成),請根據圖中信息,解答下列問題:
(1)此次共調查了 名學生;
(2)將條形統計圖補充完整;
(3)圖2中“小說類”所在扇形的圓心角為 度;
(4)若該校共有學生2500人,估計該校喜歡“社科類”書籍的學生人數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】廣州融創樂園是國內首個以南越文化、嶺南風格為主題的游樂園,自2019年6月開園以來受到了國內外游客的熱捧.某旅游團組織一批游客游玩了樂園內的四個網紅項目,“A.雙龍飛舞”、“B.飛躍廣東”、“C.云霄塔”、“D.怒海狂濤”,并進行了“我最喜歡的一個項目”的投票評選活動,投票結果繪制成以下兩幅尚未完整的統計圖.請你根據圖中提供的信息,解答下列問題:
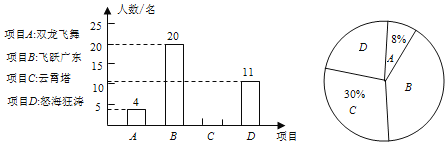
(1)參與投票的游客總人數為 人;
(2)扇形統計圖中B所對的圓心角度數為 度,并補全條形統計圖;
(3)從投票給“雙龍飛舞“的3名男生和1名女生中隨機抽取2名了解情況,請你用列舉法求恰好抽到1男1女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新學期,某校開設了“防疫宣傳”“心理疏導”等課程.為了解學生對新開設課程的掌握情況,從八年級學生中隨機抽取了部分學生進行了一次綜合測試.測試結果分為四個等級:A級為優秀,B級為良好,C級為及格,D級為不及格.將測試結果繪制了如圖兩幅不完整的統計圖.根據統計圖中的信息解答下列問題:
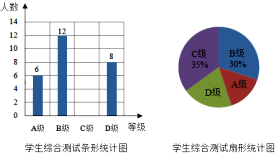
(1)本次抽樣測試的學生人數是________名;
(2)扇形統計圖中表示A級的扇形圓心角α的度數是________,并把條形統計圖補充完整;
(3)該校八年級共有學生500名,如果全部參加這次測試,估計優秀的人數為____;
(4)某班有4名優秀的同學(分別記為E,F,G,H,其中E為小明),班主任要從中隨機選擇兩名同學進行經驗分享.利用列表法或畫樹狀圖法,求小明被選中的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
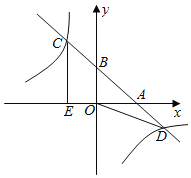
【題目】如圖,直線y=﹣x+b與x、y軸的正半軸交于點A,B,與雙曲線y=﹣![]() 交于點C(點C在第二象限內),點D,過點C作CE⊥x軸于點E,記四邊形OBCE的面積為S1,△OBD的面積為S2,若
交于點C(點C在第二象限內),點D,過點C作CE⊥x軸于點E,記四邊形OBCE的面積為S1,△OBD的面積為S2,若![]() =
=![]() ,則b的值為_____.
,則b的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
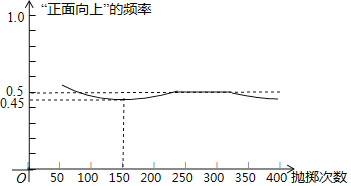
【題目】如圖顯示了用計算機模擬隨機拋擲一枚硬幣的某次實驗的結果
下面有三個推斷:
①當拋擲次數是100時,計算機記錄“正面向上”的次數是47,所以“正面向上”的概率是0.47;
②隨著試驗次數的增加,“正面向上”的頻率總在0.5附近擺動,顯示出一定的穩定性,可以估計“正面向上”的概率是0.5;
③若再次用計算機模擬此實驗,則當拋擲次數為150時,“正面向上”的頻率一定是0.45.
其中合理的是( )
A.①B.②C.①②D.①③
查看答案和解析>>
科目:初中數學 來源: 題型:
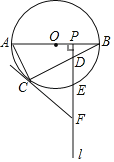
【題目】如圖,![]() 是
是![]() 的直徑,
的直徑,![]() 為
為![]() 上一點,
上一點,![]() 是半徑
是半徑![]() 上一動點(不與
上一動點(不與![]() ,
,![]() 重合),過點
重合),過點![]() 作射線
作射線![]() ,分別交弦
,分別交弦![]() ,
,![]() 于
于![]() ,
,![]() 兩點,過點
兩點,過點![]() 的切線交射線
的切線交射線![]() 于點
于點![]() .
.
(1)求證:![]() .
.
(2)當![]() 是
是![]() 的中點時,
的中點時,
①若![]() ,試證明四邊形
,試證明四邊形![]() 為菱形;
為菱形;
②若![]() ,且
,且![]() ,求
,求![]() 的長度.
的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com