
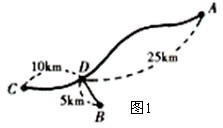
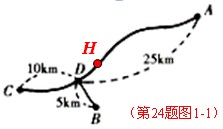
如圖1,![]() 為三個超市,在
為三個超市,在![]() 通往
通往![]() 的道路(粗實線部分)上有一
的道路(粗實線部分)上有一![]() 點,
點,![]() 與
與![]() 有道路(細實線部分)相通.
有道路(細實線部分)相通.![]() 與
與![]() ,
,![]() 與
與![]() ,
,![]() 與
與![]() 之間的路程分別為
之間的路程分別為![]() ,
,![]() ,
,![]() .現計劃在
.現計劃在![]() 通往
通往![]() 的道路上建一個配貨中心
的道路上建一個配貨中心![]() ,每天有一輛貨車只為這三個超市送貨.該貨車每天從
,每天有一輛貨車只為這三個超市送貨.該貨車每天從![]() 出發,單獨為
出發,單獨為![]() 送貨
送貨![]() 次,為
次,為![]() 送貨
送貨![]() 次,為
次,為![]() 送貨
送貨![]() 次.貨車每次僅能給一家超市送貨,每次送貨后均返回配貨中心
次.貨車每次僅能給一家超市送貨,每次送貨后均返回配貨中心![]() .設
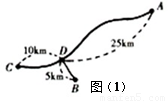
.設![]() 到
到![]() 的路程為
的路程為![]() .這輛貨車每天行駛的路程為
.這輛貨車每天行駛的路程為![]() .
.
(1)用含x的代數式填空:
 當
當![]() 時,貨車從
時,貨車從![]() 到
到![]() 往返
往返![]() 次的路程為
次的路程為![]() .
.
貨車![]() 從
從![]() 到
到![]() 往返
往返![]() 次的路程為_______
次的路程為_______![]() .
.
 貨車從
貨車從![]() 到
到![]() 往返
往返![]() 次
次![]() 的路程為_______
的路程為_______![]() .
.
這輛貨車每天行駛的路程![]() __________.
__________.
當![]() 時,
時,
這輛貨車每天行駛的路程![]() _________;
_________;
(2)請在圖2中畫出![]() 與
與![]() (
(![]() )的函數圖象;
)的函數圖象;
(3)配貨中心![]() 建在哪段,這輛貨車每天行駛的路程最短?
建在哪段,這輛貨車每天行駛的路程最短?
[答案](1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)如圖2-1;(3)
;(2)如圖2-1;(3)![]() .
.
[考點] 一次函數:一次函數的運用:根據題意列出一次函數,確定自變量的取舍范圍;作一次函數圖象.
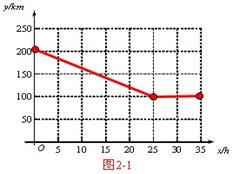
[解析] 因為![]() 與
與![]() 之間的路程為
之間的路程為![]() ,當
,當![]() 時,
時,![]() 在
在![]() 與
與![]() 路段上,如圖(第24題圖1-1),又,
路段上,如圖(第24題圖1-1),又,![]() 與
與![]() 之間的路程為
之間的路程為![]() ,此時,
,此時,
貨車從![]() 到
到![]() 往返
往返![]() 次的路程為
次的路程為![]() ,從
,從![]() 到
到![]() 往返
往返![]() 次的路程為:
次的路程為:![]() .
.
貨車從![]() 與
與![]() 之間的路程為
之間的路程為![]() ,
,![]() 到
到![]() 往返
往返![]() 次的路程為:
次的路程為:
![]() ;
;
這輛貨車每天行駛的路程:![]() .
.
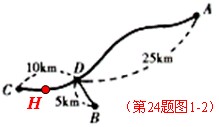
當![]() 時,
時,![]() 在
在![]() 與
與![]() 路段上,如圖(第24題圖1-2),此時,貨車從
路段上,如圖(第24題圖1-2),此時,貨車從![]() 到
到![]() 往返
往返![]() 次的路程為:
次的路程為:![]() ,從
,從![]() 到
到![]() 往返
往返![]() 次的路程還是
次的路程還是![]() ;這輛貨車每天行駛的路程為:
;這輛貨車每天行駛的路程為:![]() .
.
(2)由(1)得![]() 與
與![]() (
(![]() )的解析式為:
)的解析式為:
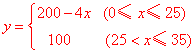
描點作出相應圖象如圖(第24題圖2-1).;
(3)由(1)(2)得知,當![]() 時,
時,![]() ,所以,只要配貨中心
,所以,只要配貨中心![]() 建在
建在![]() 與
與![]() 之間(包括
之間(包括![]() 、
、![]() )的路段上,這輛貨車每天行駛的路程都是
)的路段上,這輛貨車每天行駛的路程都是![]() ,為最短路程.
,為最短路程.


科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:吉林省中考真題 題型:計算題
 為三個超市,在
為三個超市,在 通往
通往 的道路(粗實線部分)上有一
的道路(粗實線部分)上有一 點,
點, 與
與 有道路(細實線部分)相通.
有道路(細實線部分)相通. 與
與 ,
, 與
與 ,
, 與
與 之間的路程分別為
之間的路程分別為 ,
, ,
, .現計劃在
.現計劃在 通往
通往 的道路上建一個配貨中心
的道路上建一個配貨中心 ,每天有一輛貨車只為這三個超市送貨.該貨車每天從
,每天有一輛貨車只為這三個超市送貨.該貨車每天從 出發,單獨為
出發,單獨為 送貨
送貨 次,為
次,為 送貨
送貨 次,為
次,為 送貨
送貨 次.貨車每次僅能給一家超市送貨,每次送貨后均返回配貨中心
次.貨車每次僅能給一家超市送貨,每次送貨后均返回配貨中心 .設
.設 到
到 的路程為
的路程為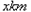 .這輛貨車每天行駛的路
.這輛貨車每天行駛的路 程為
程為 .
. 時,貨車從
時,貨車從 到
到 往返
往返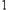 次的路程為
次的路程為 .
.
 到
到 往返
往返 次的路程為_______
次的路程為_______ .
. 到
到 往返
往返
 次的路程為_______
次的路程為_______ .
.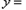 __________.
__________.
 時,
時, 
 _________;
_________; 出
出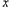 與
與 (
( )的函數圖象;
)的函數圖象;
查看答案和解析>>
科目:初中數學 來源:2012-2013學年江蘇省儀征市八年級上學期末考試數學試卷(解析版) 題型:解答題
如圖(1),A、B、C為三個超市,在A通往C的道路(粗實線部分)上有一D點,D與B有道路(細實線部分)相通.A與D、D與C、D與B之間的路程分別為25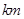 、10
、10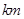 、5
、5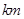 .現計劃在A通往C的道路上建一個配貨中心H,每天有一輛貨車只為這三個超市送貨.該貨車每天從H出發,單獨為A送貨1次,為B送貨1次,為C送貨2次.貨車每次僅能給一家超市送貨,每次送貨后均返回配貨中心H,設H到A的路程為
.現計劃在A通往C的道路上建一個配貨中心H,每天有一輛貨車只為這三個超市送貨.該貨車每天從H出發,單獨為A送貨1次,為B送貨1次,為C送貨2次.貨車每次僅能給一家超市送貨,每次送貨后均返回配貨中心H,設H到A的路程為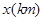 ,這輛貨車每天行駛的路程為
,這輛貨車每天行駛的路程為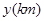 .
.
(一)用含 的代數式填空:
的代數式填空:
(1)當0≤ ≤25時,貨車從H到A往返1次的路程為
≤25時,貨車從H到A往返1次的路程為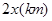
①貨車從H到B往返1次的路程為 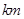 ;
;
②貨車從H到C往返2次的路程為 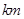 ;
;
③這輛貨車每天行駛的路程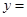
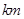 .
.
(2)當25<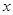 ≤35時,求這輛貨車每天行駛的路程
≤35時,求這輛貨車每天行駛的路程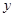 .
.
(二)請在圖(2)中畫出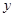 與
與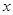 (0≤
(0≤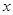 ≤35)的函數圖象;
≤35)的函數圖象;

(三)直接寫出配貨中心H建在哪段,使得這輛貨車每天行駛的路程最短.
查看答案和解析>>
科目:初中數學 來源: 題型:
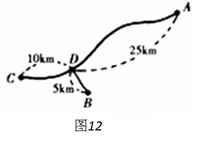
如圖12,![]() 為三個超市,在
為三個超市,在![]() 通往
通往![]() 的道路(粗實線部分)上有
的道路(粗實線部分)上有![]() 一
一![]() 點,
點,![]() 與
與![]() 有道路(細實線部分)相通.
有道路(細實線部分)相通.![]() 與
與![]() ,
,![]() 與
與![]() ,
,![]() 與
與![]() 之間的路程分別為
之間的路程分別為![]() ,
,![]() ,
,![]() .現計劃在
.現計劃在![]() 通往
通往![]() 的道路上建一個配貨中心
的道路上建一個配貨中心![]() ,每天有一輛貨車只為這三個超市送貨.該貨車每天從
,每天有一輛貨車只為這三個超市送貨.該貨車每天從![]() 出發,單獨為
出發,單獨為![]() 送貨
送貨![]() 次,為
次,為![]() 送貨
送貨![]() 次,為
次,為![]() 送貨
送貨![]() 次.貨車每次僅能給一家超市送貨,每次送貨后均返回配貨中心
次.貨車每次僅能給一家超市送貨,每次送貨后均返回配貨中心![]() .設
.設![]() 到
到![]() 的路程為
的路程為![]() .這輛貨車每天行駛的路
.這輛貨車每天行駛的路![]() 程為
程為![]() .
.
(1)用含x的代數式填空:
當![]() 時,貨車從
時,貨車從![]() 到
到![]() 往返
往返![]() 次的路程為
次的路程為![]() .
.
貨車![]() 從
從![]() 到
到![]() 往返
往返![]() 次的路程為_______
次的路程為_______![]() .
.
貨車從![]() 到
到![]() 往返
往返![]() 次
次![]() 的路程為_______
的路程為_______![]() .
.
這輛貨車每天行駛的路程![]() __________.
__________.
當![]() 時,
時,
這輛貨車每天行駛的![]() 路程
路程![]() _________;
_________;
(2)請在圖13中畫![]() 出
出![]() 與
與![]() (
(![]() )的函數圖象;
)的函數圖象;
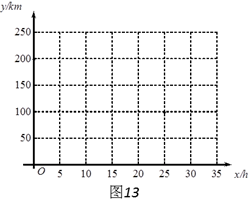 (3)配貨中心
(3)配貨中心![]() 建在哪段,這輛貨車每天行駛的路程最短?
建在哪段,這輛貨車每天行駛的路程最短?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com