
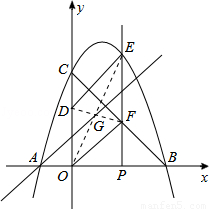
如圖,拋物線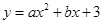 與
與 軸相交于點
軸相交于點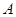 (﹣1,0)、
(﹣1,0)、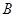 (3,0),與
(3,0),與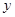 軸相交于點
軸相交于點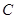 ,點
,點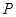 為線段
為線段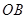 上的動點(不與
上的動點(不與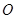 、
、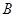 重合),過點
重合),過點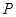 垂直于
垂直于 軸的直線與拋物線及線段
軸的直線與拋物線及線段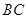 分別交于點
分別交于點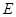 、
、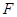 ,點
,點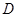 在
在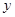 軸正半軸上,
軸正半軸上,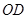 =2,連接
=2,連接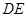 、
、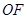 .
.
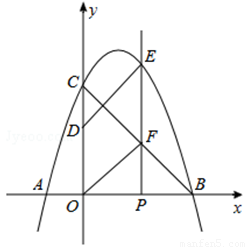
(1)求拋物線的解析式;
(2)當四邊形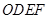 是平行四邊形時,求點
是平行四邊形時,求點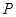 的坐標;
的坐標;
(3)過點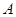 的直線將(2)中的平行四邊形
的直線將(2)中的平行四邊形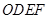 分成面積相等的兩部分,求這條直線的解析式.(不必說明平分平行四邊形面積的理由)
分成面積相等的兩部分,求這條直線的解析式.(不必說明平分平行四邊形面積的理由)
(1)拋物線的解析式為: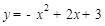 ;(2)
;(2)  點坐標為
點坐標為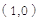 或
或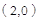 ;(3) ①當
;(3) ①當
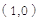 時,所求直線的解析式為:
時,所求直線的解析式為: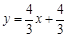 ;②當
;②當
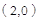 時,所求直線的解析式為:
時,所求直線的解析式為: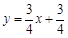 .
.
【解析】
試題分析:
(1)將點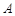 和點
和點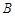 的坐標代入拋物線函數中,可求出未知量
的坐標代入拋物線函數中,可求出未知量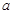 ,
,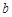 .則可求出該拋物線解析式;(2)由平行四邊形的性質可知,
.則可求出該拋物線解析式;(2)由平行四邊形的性質可知,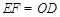 ,用含未知量
,用含未知量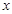 的代數式表示
的代數式表示 的長度。則可得點
的長度。則可得點 坐標
;(3)平行四邊形是中心對稱圖形,其對稱中心為兩條對角線的交點(或對角線的中點),過對稱中心的直線平分平行四邊形的面積,因此過點
坐標
;(3)平行四邊形是中心對稱圖形,其對稱中心為兩條對角線的交點(或對角線的中點),過對稱中心的直線平分平行四邊形的面積,因此過點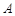 與
與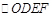 對稱中心的直線平分
對稱中心的直線平分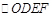 的面積.求得此直線,首先要求得
的面積.求得此直線,首先要求得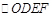 對稱中心的坐標.則兩點坐標可確定該直線.
對稱中心的坐標.則兩點坐標可確定該直線.
試題解析:
(1) 點
點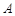
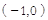 、
、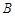
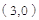 在拋物線
在拋物線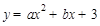 上,
上,
∴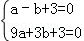 ,
,
解得 ,
,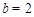 ,
,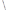 拋物線的解析式為:
拋物線的解析式為: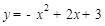 .
.
(2)在拋物線解析式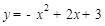 中,令
中,令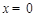 ,得
,得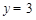 ,
,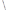
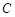
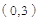 .
.
設直線BC的解析式為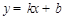 ,將
,將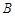
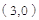 ,
,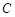
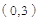 坐標代入得:
坐標代入得:
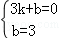 ,解得
,解得 ,
,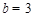 ,∴
,∴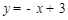 .
.
設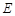 點坐標為
點坐標為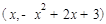 ,則
,則
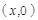 ,
,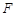
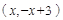 ,
,
∴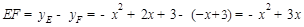
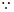 四邊形
四邊形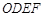 是平行四邊形,
是平行四邊形,
∴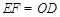 ,
,
∴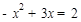 ,即
,即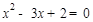 ,
,
解得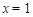 或
或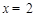 ,
,
∴ 點坐標為
點坐標為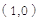 或
或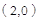 .
.
(3)平行四邊形是中心對稱圖形,其對稱中心為兩條對角線的交點(或對角線的中點),過對稱中心的直線平分平行四邊形的面積,因此過點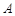 與
與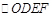 對稱中心的直線平分
對稱中心的直線平分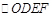 的面積.
的面積.
①當
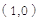 時,點
時,點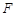 坐標為
坐標為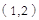 ,又
,又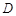
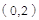
設對角線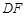 的中點為
的中點為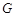 ,則
,則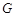
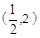 .
.
設直線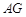 的解析式為
的解析式為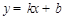 ,將
,將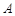
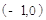 ,
,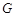
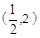 坐標代入得:
坐標代入得:
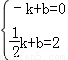 ,
,
解得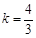 ,
,
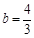 ,∴所求直線的解析式為:
,∴所求直線的解析式為: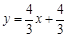 ;
;
②當
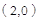 時,
時,
點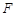 坐標為
坐標為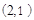 ,又
,又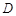
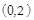 ,
,
設對角線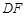 的中點為
的中點為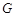 ,則
,則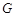
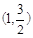 .
.
設直線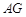 的解析式為
的解析式為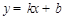 ,將
,將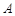
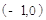 ,
,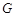
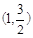 坐標代入得:
坐標代入得:
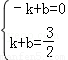 ,解得
,解得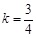 ,
,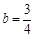 ,
,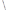 所求直線的解析式為:
所求直線的解析式為: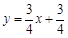 .
.
綜上所述,所求直線的解析式為: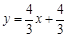 或
或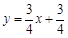 .
.
【考點】1.一次函數解析式的解法;2.二次函數解析式的解法.


 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案 課堂練加測系列答案
課堂練加測系列答案 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案科目:初中數學 來源: 題型:
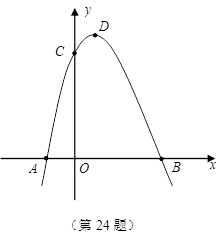
如圖,拋物線與
軸相交于
、
兩點(點
在點
的左側),與
軸相交于點
,頂點為
.
(1)直接寫出、
、
三點的坐標和拋物線的對稱軸;
(2)連接,與拋物線的對稱軸交于點
,點
為線段
上的一個動點,過點
作
交拋物線于點
,設點
的橫坐標為
;
①用含的代數式表示線段
的長,并求出當
為何值時,四邊形
為平行四邊形?
②設的面積為
,求
與
的函數關系式
查看答案和解析>>
科目:初中數學 來源:2012屆江蘇省泰興市黃橋區九年級中考一模數學試卷(帶解析) 題型:解答題
如圖,拋物線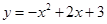 與
與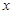 軸相交于
軸相交于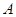 、
、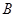 兩點(點
兩點(點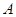 在點
在點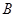 的左側),與
的左側),與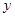 軸相交于點
軸相交于點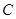 ,頂點為
,頂點為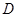 .
.
【小題1】直接寫出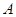 、
、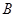 、
、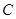 三點的坐標和拋物線的對稱軸;
三點的坐標和拋物線的對稱軸;
【小題2】連接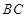 ,與拋物線的對稱軸交于點
,與拋物線的對稱軸交于點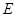 ,點
,點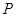 為線段
為線段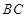 上的一個動點,過點
上的一個動點,過點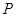 作
作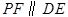 交拋物線于點
交拋物線于點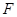 ,設點
,設點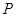 的橫坐標為
的橫坐標為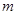 ;
;
①用含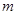 的代數式表示線段
的代數式表示線段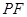 的長,并求出當
的長,并求出當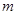 為何值時,四邊形
為何值時,四邊形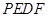 為平行四邊形?
為平行四邊形?
②設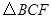 的面積為
的面積為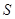 ,求
,求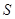 與
與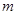 的函數關系式.
的函數關系式.
查看答案和解析>>
科目:初中數學 來源:2013屆福建省泉州市洛江區初三上學期期末質量檢測數學試卷(帶解析) 題型:解答題
如圖,拋物線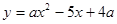 與
與 軸相交于點
軸相交于點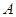 、
、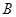 ,且經過點
,且經過點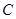 (5,4).該拋物線頂點為
(5,4).該拋物線頂點為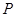 .
.
(1)求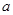 的值和該拋物線頂點
的值和該拋物線頂點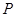 的坐標.
的坐標.
(2)求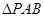 的面積;
的面積;
(3)若將該拋物線先向左平移4個單位,再向上平移2個單位,求出平移后拋物線的解析式.
查看答案和解析>>
科目:初中數學 來源:2011-2012學年江蘇省泰興市黃橋區九年級中考一模數學試卷(解析版) 題型:解答題
如圖,拋物線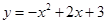 與
與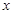 軸相交于
軸相交于 、
、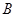 兩點(點
兩點(點 在點
在點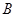 的左側),與
的左側),與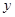 軸相交于點
軸相交于點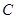 ,頂點為
,頂點為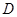 .
.

1.直接寫出 、
、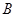 、
、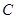 三點的坐標和拋物線的對稱軸;
三點的坐標和拋物線的對稱軸;
2.連接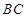 ,與拋物線的對稱軸交于點
,與拋物線的對稱軸交于點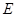 ,點
,點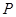 為線段
為線段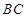 上的一個動點,過點
上的一個動點,過點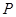 作
作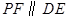 交拋物線于點
交拋物線于點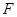 ,設點
,設點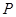 的橫坐標為
的橫坐標為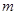 ;
;
①用含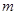 的代數式表示線段
的代數式表示線段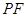 的長,并求出當
的長,并求出當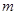 為何值時,四邊形
為何值時,四邊形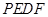 為平行四邊形?
為平行四邊形?
②設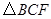 的面積為
的面積為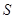 ,求
,求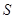 與
與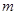 的函數關系式.
的函數關系式.
查看答案和解析>>
科目:初中數學 來源:2010-2011年重慶一中初三下學期第一次考前模擬數學試卷 題型:解答題
如圖,拋物線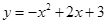 與
與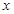 軸相交于
軸相交于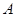 、
、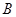 兩點(點
兩點(點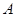 在點
在點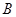 的左側),與
的左側),與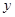 軸相交于點
軸相交于點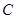 ,頂點為
,頂點為 .
.
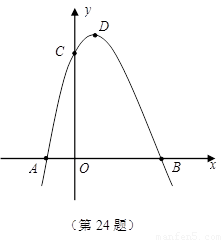
(1)直接寫出 、
、 、
、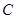 三點的坐標和拋物線的對稱軸;
三點的坐標和拋物線的對稱軸;
(2)連接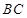 ,與拋物線的對稱軸交于點
,與拋物線的對稱軸交于點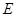 ,點
,點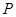 為線段
為線段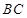 上的一個動點,過點
上的一個動點,過點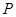 作
作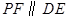 交拋物線于點
交拋物線于點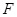 ,設點
,設點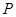 的橫坐標為
的橫坐標為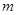 ;
;
①用含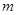 的代數式表示線段
的代數式表示線段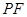 的長,并求出當
的長,并求出當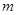 為何值時,四邊形
為何值時,四邊形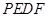 為平行四邊形?
為平行四邊形?
②設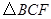 的面積為
的面積為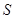 ,求
,求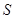 與
與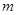 的函數關系式
的函數關系式
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com