
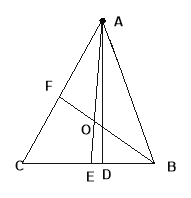
【題目】如圖,△ABC中,AD是高,AE、BF是角平分線,它們相交于點O,∠CAB=500,∠C=600,求∠DAE和∠BOA的度數。
【答案】
解:∵∠A=50°,∠C=60°
∴∠ABC=180°-50°-60°=70°,
又∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°-90°-∠C=30°,
∵AE、BF是角平分線,
∴∠CBF=∠ABF=35°,∠EAF=25°,
∴∠DAE=∠DAC-∠EAF=5°,
∠AFB=∠C+∠CBF=60°+35°=95°,
∴∠BOA=∠EAF+∠AFB=25°+95°=120°,
∴∠DAC=30°,∠BOA=120°.
故∠DAE=5°,∠BOA=120°.
【解析】先利用三角形內角和定理可求∠ABC,在直角三角形ACD中,易求∠DAC;再根據角平分線定義可求∠CBF、∠EAF,可得∠DAE的度數;然后利用三角形外角性質,可先求∠AFB,再次利用三角形外角性質,容易求出∠BOA.


 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:初中數學 來源: 題型:
【題目】安寧市的一種綠色蔬菜,若在市場上直接銷售,每噸利潤為1000元,若經粗加工后銷售,每噸利潤可達4500元;若經精加工后銷售每噸獲利7500元.當地一家農產品企業收購這種蔬菜140噸,該企業加工廠的生產能力是:如果對蔬菜進行粗加工,每天可以加工16噸,如果進行精加工,每天可加工6噸,但兩種加工方式不能同時進行,受季節條件限制,企業必須在15天的時間將這批蔬菜全部銷售或加工完畢,企業研制了四種可行方案: 方案一:全部直接銷售;
方案二:全部進行粗加工;
方案三:盡可能多地進行精加工,沒有來得及進行精加工的直接銷售;
方案四:將一部分進行精加工,其余的進行粗加工,并恰好15天完成.
請通過計算以上四個方案的利潤,幫助企業選擇一個最佳方案使所獲利潤最多?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD,BE分別為邊BC,AC上的高線,D,E為垂足,M為AB的中點,N為DE的中點.求證:
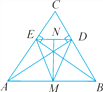
(1)△MDE是等腰三角形.
(2)MN⊥DE.
查看答案和解析>>
科目:初中數學 來源: 題型:
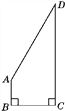
【題目】某校一塊空地被荒廢,如圖,為了綠化環境,學校打算利用這塊空地種植花草,已知AB⊥BC,CD⊥BC,AB=![]() CD=
CD=![]() m,BC=3
m,BC=3![]() m,試求這塊空地的面積.
m,試求這塊空地的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列作圖語句正確的是( )
A. 作射線AB,使AB=a B. 作∠AOB=∠a
C. 延長直線AB到點C,使AC=BC D. 以點O為圓心作弧
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com