
【題目】如圖,拋物線![]() 與坐標軸交于點
與坐標軸交于點![]() ,點
,點![]() 和點
和點![]() ,連接
,連接![]() .
.
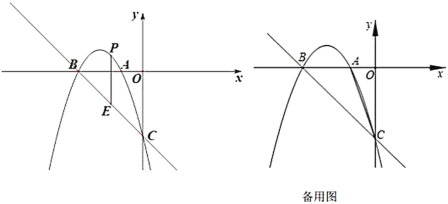
(1)求拋物線的解析式;
(2)如圖,已知點![]() 在線段
在線段![]() 的上方(不包括點
的上方(不包括點![]() 和點
和點![]() ),過
),過![]() 點作
點作![]() 軸的垂線交直線
軸的垂線交直線![]() 于點
于點![]() ,求線段
,求線段![]() 的最大值;
的最大值;
(3)該拋物線上是否存在點![]() ,使得
,使得![]() ?若存在,求點
?若存在,求點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)當
;(2)當![]() 時,
時,![]() 有最大值,最大值為
有最大值,最大值為![]() ;(3)存在,點
;(3)存在,點![]() 的坐標為
的坐標為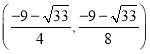 、
、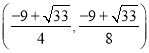 、
、![]() 或
或![]() .
.
【解析】
(1)把![]() ,點
,點![]() 和點
和點![]() 代入拋物線解析式
代入拋物線解析式![]() 組成三元一次方程組,解方程組,即可得拋物線的系數a、b、c的值,代入拋物線解析式即可.
組成三元一次方程組,解方程組,即可得拋物線的系數a、b、c的值,代入拋物線解析式即可.
(2)因為點P在拋物線上,所以設![]() ,而
,而![]() 的直線方程為
的直線方程為![]() ,所以
,所以![]() ,所以
,所以![]() ,利用二次函數性質求得PE的最大值為;
,利用二次函數性質求得PE的最大值為;
(3)過點![]() 作
作![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,由題意求得
,由題意求得![]() ,再根據相似三角形的性質可得
,再根據相似三角形的性質可得![]() ,
,![]() ,進而證出
,進而證出![]() 是等腰直角三角
是等腰直角三角![]()
![]() ,從而求得
,從而求得![]() ,設
,設![]() ,①當
,①當![]() 或
或![]() 時,點
時,點![]() 在點
在點![]() 左側或在
左側或在![]() 之間,橫縱坐標均為負數,
之間,橫縱坐標均為負數,![]() ,
,![]() ,所以
,所以![]() ,列方程解即可得P的坐標;②當
,列方程解即可得P的坐標;②當![]() 或
或![]() 時,點
時,點![]() 在
在![]() 之間或在點
之間或在點![]() 右側,橫縱坐標異號
右側,橫縱坐標異號![]() ,列方程即可得P點的坐標;
,列方程即可得P點的坐標;
(1)∵拋物線與![]() 軸交于點
軸交于點![]() ,點
,點![]() ,與y軸交于點
,與y軸交于點![]()
∴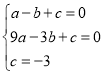
∴
∴拋物線解析式為![]()
(2)設![]() ,
,![]() 的直線方程為
的直線方程為![]()
∴![]() ,∴
,∴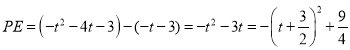
當![]() 時,
時,![]() 有最大值,最大值為
有最大值,最大值為![]()
(3)如圖1,過點![]() 作
作![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]()

∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]() ,
,![]()
∴![]() 是等腰直角三角形∴
是等腰直角三角形∴![]()
∴![]()
∴![]()
∴![]()
設![]()
①當![]() 或
或![]() 時,點
時,點![]() 在點
在點![]() 左側或在
左側或在![]() 之間,橫縱坐標均為負數
之間,橫縱坐標均為負數
∴![]() ,
,![]()
∴![]()
解得:![]() ,,
,,![]()
 或
或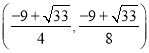
②當![]() 或
或![]() 時,點
時,點![]() 在
在![]() 之間或在點
之間或在點![]() 右側,橫縱坐標異號
右側,橫縱坐標異號
∴![]()
解得:![]() ,
,![]()
∴![]() 或
或![]()
綜上所述,點![]() 的坐標為
的坐標為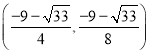 、
、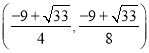 、
、![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】某學校為了解九年級的600名學生每天的自主學習情況,隨機抽查了九年級的部分學生,并調查他們每天自主學習的時間.根據調查結果,制作了兩副不完整的統計圖(圖1圖2),請根據統計圖中的信息回答下列問題:
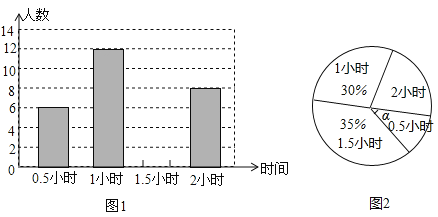
(1)本次調查的學生人數是 人;
(2)圖2中角![]() 是 度;
是 度;
(3)將圖1條形統計圖補充完整;
(4)估算該校九年級學生自主學習不少于1.5小時有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表記錄了甲、乙、丙、丁四名同學最近幾次數學考試成績的平均數與方差.根據表中數據,要從中選擇一名成績好且發揮穩定的同學參加數學競賽,應該選擇__________(填“甲”, “乙”, “丙”, “丁”).
甲 | 乙 | 丙 | 丁 | |
平均數(分) | 92 | 95 | 95 | 92 |
方差 | 3.6 | 3.6 | 7.4 | 8.1 |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,AB=5cm,BD=8cm.點P從點B出發,沿BA方向勻速運動,速度為![]() ;同時,點Q從點D出發,沿DA方向勻速運動,速度為1cm/s.過點P作PN∥BC分別交BD,CD于點M,N,連接QM,QN.設運動時間為
;同時,點Q從點D出發,沿DA方向勻速運動,速度為1cm/s.過點P作PN∥BC分別交BD,CD于點M,N,連接QM,QN.設運動時間為![]() .解答下列問題:
.解答下列問題:
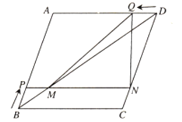
(1)當![]() 為何值時,點
為何值時,點![]() 在線段
在線段![]() 的垂直平分線上?
的垂直平分線上?
(2)設![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 的函數關系式;
的函數關系式;
(3)在運動過程中,是否存在某一時刻![]() ,使
,使![]() 的面積為菱形
的面積為菱形![]() 面積的
面積的![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(4)是否存在某一時刻![]() ,使
,使![]() 為等腰三角形?若存在,請直接寫出
為等腰三角形?若存在,請直接寫出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
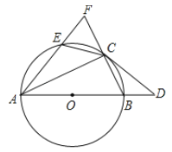
【題目】如圖,E為圓O上的一點,C為劣弧EB的中點.CD切![]() 于點C,交
于點C,交![]() 的直徑AB的延長線于點D.延長線段AE和線段BC,使之交于點F.
的直徑AB的延長線于點D.延長線段AE和線段BC,使之交于點F.
(1)求證:![]() 和
和![]() 都是等腰三角形;
都是等腰三角形;
(3)若![]() ,
,![]() ,求EF的長.
,求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市計劃購進一批A、B兩種規格的端午節禮盤進行銷售,進價和售價如下表所示:
端午節禮盤規格 | A | B |
進價(元/盤) | 80 | 100 |
售價(元/盤) | 120 | 160 |
若購進兩種規格的端午節禮盒共300盒,且投入資金不超過26800元.
(1)該超市應購進A規格端午節禮盒至少多少盒?
(2)若超市購進A規格端午節禮盒的進價每盒降低a元,并保持這兩個規格的端午節禮盒的售價不變,且最多購進240盒A規格端午節禮盒.如果這批端午節禮盒售出后,超市剛好獲利18480元,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,D是AC邊上的中點,連結BD,把△BDC′沿BD翻折,得到△![]() ,DC與AB交于點E,連結
,DC與AB交于點E,連結![]() ,若AD=AC′=2,BD=3則點D到BC的距離為( )
,若AD=AC′=2,BD=3則點D到BC的距離為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】鐘南山院士談到防護新型冠狀病毒肺炎時說:“我們需要重視防護,但也不必恐慌,盡量少去人員密集的場所,出門戴口罩,在室內注意通風,勤洗手,多運動,少熬夜.”某學校為了了解學生對新型冠狀病毒肺炎防護知識的掌握情況,隨機抽取若干名同學利用網絡進行了“新冠狀病毒肺炎防疫知識”問卷測試.根據測試成績分布情況,他們將全部測試成績分成![]() 、
、![]() 、
、![]() 、
、![]() 四組,繪制了如下統計圖表:
四組,繪制了如下統計圖表:
“新冠狀病毒肺炎防疫知識”問卷測試成績統計表
組別 | 分數/分 | 頻數 | 各組總分/分 |
|
| 38 | 2581 |
|
|
| 5543 |
|
| 60 | 5100 |
|
| 30 | 2796 |
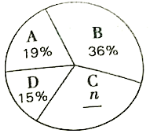
依據以上統計信息,解答下列問題:
(1)求得![]() ,
,![]() ;
;
(2)這次測試成績的中位數落在 組;
(3)求本次全部測試成績的平均數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com