
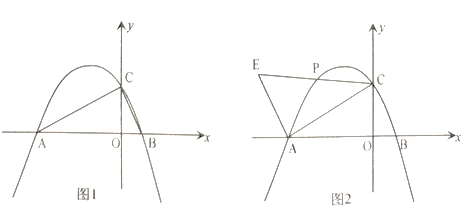
【題目】如圖1,已知開口向下的拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() 不小于
不小于![]() .
.
(1)求點![]() 的坐標(用含
的坐標(用含![]() 的代數式表示);
的代數式表示);
(2)求系數![]() 的取值范圍;
的取值范圍;
請你根據自身能力從![]() 或(4)小題中任選-題作答.
或(4)小題中任選-題作答.
(3)如圖2,當![]() 時,
時,![]() 為直線
為直線![]() 上方拋物線上一動點,過點
上方拋物線上一動點,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() 試探究是否存在點
試探究是否存在點![]() ,使得
,使得![]() 的某一個角等于
的某一個角等于![]() 的
的![]() 倍?若存在,求點
倍?若存在,求點![]() 的橫坐標;若不存在,請說明理由.
的橫坐標;若不存在,請說明理由.
(4)如圖2,當![]() 時,
時,![]() 為直線
為直線![]() 上方拋物線上一動點,過點
上方拋物線上一動點,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() 拋物線的對稱軸與
拋物線的對稱軸與![]() 軸交于點
軸交于點![]() 連接
連接![]() 試探究是否存在點
試探究是否存在點![]() 使得
使得![]() 與
與![]() 相似?若存在,求點
相似?若存在,求點![]() 的橫坐標;若不存在,請說明理由.
的橫坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在符合條件的兩點
;(3)存在符合條件的兩點![]() ,其橫坐標為
,其橫坐標為![]() 或
或![]() ;(4)存在符合條件的兩點
;(4)存在符合條件的兩點![]() 其橫坐標為
其橫坐標為![]() 或
或![]() .
.
【解析】
(1)令y=0,求解即可得到A、B的坐標;令x=0,即可求得C點坐標,進而得到答案;
(2)先證明 ![]() ,根據相似三角形的性質得到
,根據相似三角形的性質得到![]() ,求出OC的長度,再根據
,求出OC的長度,再根據![]() 不小于90°得到
不小于90°得到![]() 即可求出a的范圍;
即可求出a的范圍;
(3)在![]() 上取點
上取點![]() 使
使![]() 得到
得到![]() 根據勾股定理求出
根據勾股定理求出![]() 的長, 根據
的長, 根據![]() 得到
得到![]() .再分情況討論即可得到答案;
.再分情況討論即可得到答案;
(4)分情況討論當![]() 得到
得到![]() 再過點
再過點![]() 作
作![]() 軸于點
軸于點![]() 求出點
求出點![]() 的坐標,進而得到P的橫坐標,再討論當
的坐標,進而得到P的橫坐標,再討論當![]() ,類似求解即可得到答案;
,類似求解即可得到答案;
![]() 令
令![]() 得
得![]()
解得![]() ,
,
令![]() 得
得![]() ,
,
![]()
![]() 當
當![]() 時,
時,
![]()
![]()
![]()
![]()
![]()
![]() 不小于
不小于![]()
![]()
![]() ,
,
![]()
又![]()
![]()
![]() 存在.當
存在.當![]() 時,
時,
![]()
![]()
![]() ,
,![]()
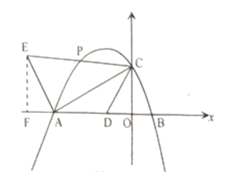
在![]() 上取點
上取點![]() 如下圖,使
如下圖,使![]()
則![]()
設![]() 的長為
的長為![]() ,則
,則![]()
在![]() 中,
中,![]()
![]()
![]()
![]() .
.
①當![]() 時,
時,![]()
![]()
![]()
![]()
過點![]() 作
作![]() 軸于點
軸于點![]()
![]() ,
,
![]()
![]()
![]()
![]()
又![]()
![]() 直線
直線![]() 的解析式為
的解析式為![]()
![]() 拋物線解析式為
拋物線解析式為![]()
![]()
![]() (舍去),
(舍去),![]()
②當![]() 時,
時,![]()
![]()
![]()
![]() 時,
時,
同上可得![]() ,直線
,直線![]() 的解析式為
的解析式為![]()
![]()
![]() (舍去),
(舍去),![]() .
.
綜上所述,存在符合條件的兩點![]()
其橫坐標為![]() 或
或![]()
![]() 存在.當
存在.當![]() 時,
時,
![]()
![]()
當![]()
即![]() 時,
時,![]()
過點![]() 作
作![]() 軸于點
軸于點![]()
![]() ,
,
![]()
![]()
![]()
![]() ,
,
又![]() ,
,
![]() 直線
直線![]() 的解析式為
的解析式為![]()
![]() 拋物線解析式為
拋物線解析式為![]()
![]()
![]() (舍去),
(舍去),![]()
當![]() ,
,
即![]() 時,
時,![]()
同上可得![]() ,
,
直線![]() 的解析式為
的解析式為![]()
![]()
![]() (舍去),
(舍去),![]()
綜上所述,存在符合條件的兩點![]() 其橫坐標為
其橫坐標為![]() 或
或![]() .
.


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案 小學期末標準試卷系列答案
小學期末標準試卷系列答案科目:初中數學 來源: 題型:
【題目】在![]() 和
和![]() 中,
中,![]() ,直線
,直線![]() 與
與![]() 交于點
交于點![]() .
.
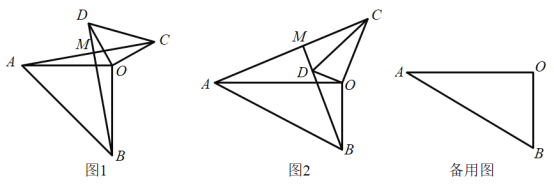
(1)如圖1,若![]() ,填空:①
,填空:①![]() 的值為____________;
的值為____________;
②![]() 的度數為___________.
的度數為___________.
(2)如圖2,若![]() ,求
,求![]() 的值(用含
的值(用含![]() 的式子表示)及
的式子表示)及![]() 的度數;
的度數;
(3)若![]() ,
,![]() ,
,![]() ,將三角形
,將三角形![]() 繞著點
繞著點![]() 在平面內旋轉,直接寫出當點
在平面內旋轉,直接寫出當點![]() 、
、![]() 、
、![]() 在同一直線上時,線段
在同一直線上時,線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
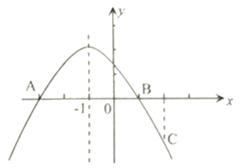
【題目】在平面直角坐標系中,二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,現給以下結論:①abc<0;②c+2a<0;③9a﹣3b+c=0;④a﹣b≥m(am+b)(m為實數);⑤4ac﹣b2<0.其中錯誤結論的個數有( )
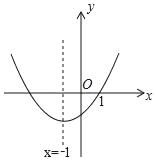
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
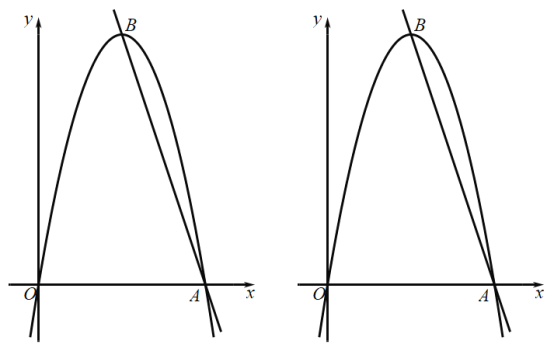
【題目】如圖,在平面直角坐標系中,拋物線![]() 與
與![]() 軸的正半軸交于點A,拋物線的頂點為B,直線
軸的正半軸交于點A,拋物線的頂點為B,直線![]() 經過A,B兩點,且
經過A,B兩點,且![]() .
.
(1)求拋物線的解析式
(2)點P在第一象限內對稱軸右側的拋物線上,其橫坐標為![]() ,連接OP,交對稱軸于點C,過點C作
,連接OP,交對稱軸于點C,過點C作![]() 軸,交直線
軸,交直線![]() 于點
于點![]() ,連接
,連接![]() ,設線段
,設線段![]() 的長為
的長為![]() ,求
,求![]() 與
與![]() 之間的函數關系式,并直接寫出自變量
之間的函數關系式,并直接寫出自變量![]() 的取值范圍;
的取值范圍;
(3)在(2)的條件下,點![]() 在線段
在線段![]() 上,連接
上,連接![]() ,交
,交![]() 于點F,點G是BE的中點,過點G作
于點F,點G是BE的中點,過點G作![]() 軸,交
軸,交![]() 的延長線于點
的延長線于點![]() ,當
,當![]() 且
且![]() 時,求點
時,求點![]() 的坐標;
的坐標;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數![]() 的圖象經過點
的圖象經過點![]() 點
點![]() ,點
,點![]() 點
點![]() 是拋物線上任意一點,有下列結論:①
是拋物線上任意一點,有下列結論:①![]() ; ②一元二次方程
; ②一元二次方程![]() 的兩個根為
的兩個根為![]() 和
和![]() ;③若
;③若![]() ,則
,則![]() ;④對于任意實數
;④對于任意實數![]()
![]() 總成立.其中正確結論的個數為 ( )
總成立.其中正確結論的個數為 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某初中學校每個年級學生剛好為500人,為了解數學史知識的普及情況,隨機從每個年級各抽10名學生進行測試,測試成績整理如下:
年級 | 學生測試成績表 | |||||||||
七年級 | 36 | 55 | 67 | 68 | 75 | 81 | 81 | 85 | 92 | 96 |
八年級 | 45 | 66 | 72 | 77 | 80 | 84 | 86 | 92 | 95 | 96 |
九年級 | 55 | 68 | 75 | 84 | 85 | 87 | 93 | 94 | 96 | 97 |
(1)估計該校學生數學史掌握水平能達到80分以上(含80分)的人數;
(2)現從成績在95分以上(含95分)的學生中,任取3名參加數學史學習的經驗匯報,求每個年級恰好都有一名學生參加的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校按照開展“陽光體育運動”的要求,決定主要開設![]() :乒乓球、
:乒乓球、![]() :籃球、
:籃球、![]() :跑步
:跑步![]() :跳繩這四種運動項目.為了了解學生喜歡哪一種項目,隨機抽取了部分學生進行調查,并將調查結果繪制成如圖所示的條形統計圖和扇形統計圖.請你結合圖中的信息解答下列問題:
:跳繩這四種運動項目.為了了解學生喜歡哪一種項目,隨機抽取了部分學生進行調查,并將調查結果繪制成如圖所示的條形統計圖和扇形統計圖.請你結合圖中的信息解答下列問題:
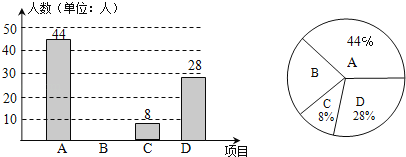
(1)樣本中喜歡![]() 項目的人數百分比是多少?其所在扇形統計圖中的圓心角的度數是多少?
項目的人數百分比是多少?其所在扇形統計圖中的圓心角的度數是多少?
(2)把條形統計圖補充完整;
(3)已知該校有1000人,請根據樣本估計全校喜歡乒乓球的人數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】張老師將自己2019年10月至2020年5月的通話時長(單位:分鐘)的有關數據整理如下:
①2019年10月至2020年3月通話時長統計表
時間 | 10月 | 11月 | 12月 | 1月 | 2月 | 3月 |
時長(單位:分鐘) | 520 | 530 | 550 | 610 | 650 | 660 |
②2020年4月與2020年5月,這兩個月通話時長的總和為1100分鐘根據以上信息,推斷張老師這八個月的通話時長的中位數可能的最大值為( )
A.550B.580C.610D.630
查看答案和解析>>
科目:初中數學 來源: 題型:
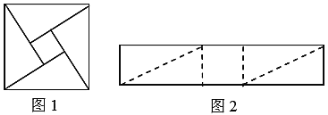
【題目】如圖1是三國時期的數學家趙爽創制的一幅“勾股圓方圖”.將圖2的矩形分割成四個全等三角形和一個正方形,恰好能拼成這樣一個“勾股圓方圖”,則該矩形與拼成的正方形的周長之比為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com