
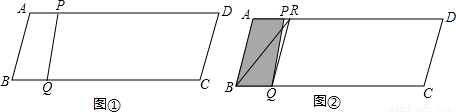
 時,根據三角形的面積公式分別求出S與t的函數關系式;
時,根據三角形的面積公式分別求出S與t的函數關系式; 時,當
時,當 <t<
<t<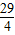 時,利用三角形的面積相等建立方程求出其解即可;
時,利用三角形的面積相等建立方程求出其解即可;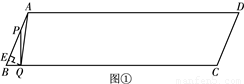
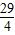 .
.
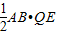 =
=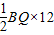 ,
,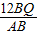 =
=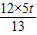 =
=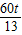 .
.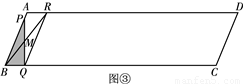
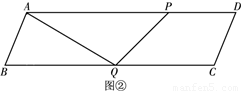
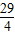 時,如圖②.
時,如圖②.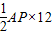 =
=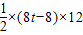 ,
, .
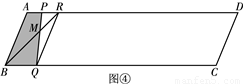
.
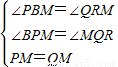 ,
,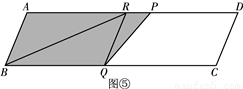
 時,如圖④.
時,如圖④.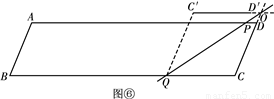
 .
. <t≤
<t≤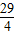 時,如圖⑤.
時,如圖⑤.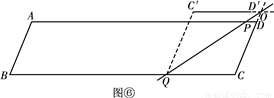
 時,線段PQ掃過的圖形(陰影部分)被線段BR分成面積相等的兩部分.
時,線段PQ掃過的圖形(陰影部分)被線段BR分成面積相等的兩部分.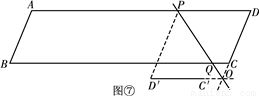
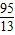 .
. .
.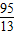 ,t=
,t=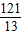 時,點C、D關于直線PQ的對稱點分別為C′、D′,且C′D′∥BC.
時,點C、D關于直線PQ的對稱點分別為C′、D′,且C′D′∥BC.

科目:初中數學 來源: 題型:
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:


查看答案和解析>>
科目:初中數學 來源: 題型:
| 2 |
 )時,作EF⊥DP于點F,連接AF,線段DF、EF與AF之間有怎樣的數量關系?直接寫出你的結論.
)時,作EF⊥DP于點F,連接AF,線段DF、EF與AF之間有怎樣的數量關系?直接寫出你的結論.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com