Question

(本題滿分10分)已知：如圖，是的直徑，是上一點，CD⊥AB，垂足為點，是 的中點，與相交于點，8 cm，cm.

【小題1】（1）求的長；
【小題2】（2）求的值.

Answer 1

【小題1】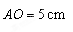
【小題2】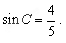

解析考點：垂徑定理；勾股定理；銳角三角函數的定義．
分析：（1）由F是的中點，根據垂徑定理的推論，得到OF⊥AC，AE=CE=4，在Rt△AEO中，利用勾股定理即可計算出OA；
（2）由CD⊥AB，利用同角的余角相等得到∠AOE=∠C，所以sinC=sin∠AOE，在Rt△AEO中，即可得到sin∠AOE的值．
解：（1）∵F是的中點，
∴=，
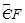又OF是半徑，
∴OF⊥AC，
∴AE=CE，
∵AC=8cm，
∴AE=4cm，
在Rt△AEO中，AE²+EO²=AO²，
又∵EF=2cm，
∴4²+（AO-2）²=AO²，解得AO=5，
∴AO=5cm．
（2）∵OE⊥AC，
∴∠A+∠AOE=90°，
∵CD⊥AB，
∴∠A+∠C=90°，（1分）
∴∠AOE=∠C，
∴sinC=sin∠AOE，
∵sin∠AOE==，
∴sinC=．