
 如圖,某點從數軸上的A點出發,第1次向右移動1個單位長度至B點,第2次從B點向左移動2個單位長度至C點,第3次從C點向右移動3個單位長度至D點,第4次從D點向左移動4個單位長度至E點,…,依此類推,經過4029或4030次移動后該點到原點的距離為2015個單位長度.
如圖,某點從數軸上的A點出發,第1次向右移動1個單位長度至B點,第2次從B點向左移動2個單位長度至C點,第3次從C點向右移動3個單位長度至D點,第4次從D點向左移動4個單位長度至E點,…,依此類推,經過4029或4030次移動后該點到原點的距離為2015個單位長度. 分析 根據數軸上點的坐標變化和平移規律(左減右加),分別求出點所對應的數,進而求出點到原點的距離;然后對奇數項、偶數項分別探究,找出其中的規律(相鄰兩數都相差3),寫出表達式就可解決問題.
解答 解:第1次點A向右移動1個單位長度至點B,則B表示的數,0+1=1;
第2次從點B向左移動2個單位長度至點C,則C表示的數為1-2=-1;
第3次從點C向右移動3個單位長度至點D,則D表示的數為-1+3=2;
第4次從點D向左移動4個單位長度至點E,則點E表示的數為2-4=-2;
第5次從點E向右移動5個單位長度至點F,則F表示的數為-2+5=3;
…;
由以上數據可知,當移動次數為奇數時,點在數軸上所表示的數滿足:$\frac{1}{2}$(n+1),
當移動次數為偶數時,點在數軸上所表示的數滿足:-$\frac{1}{2}$n,
當移動次數為奇數時,$\frac{1}{2}$(n+1)=2015,n=4029,
當移動次數為偶數時,-$\frac{1}{2}$n=-2015,n=4030.
故答案為:4029或4030.
點評 本題考查了數軸,以及用正負數可以表示具有相反意義的量,還考查了數軸上點的坐標變化和平移規律(左減右加),考查了一列數的規律探究.對這列數的奇數項、偶數項分別進行探究是解決這道題的關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
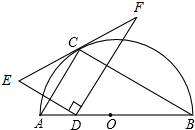 如圖點C在以AB為直徑的半圓的圓周上,若AB=4,∠ABC=30°,D為邊AB上一動點,點E和D關于AC對稱,當D與A重合時,F為EC的延長線上滿足CF=EC的點,當D與A不重合時,F為EC的延長線與過D且垂直于DE的直線的交點,
如圖點C在以AB為直徑的半圓的圓周上,若AB=4,∠ABC=30°,D為邊AB上一動點,點E和D關于AC對稱,當D與A重合時,F為EC的延長線上滿足CF=EC的點,當D與A不重合時,F為EC的延長線與過D且垂直于DE的直線的交點,查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{-a}{2b}=\frac{a}{-2b}$ | B. | $\frac{1}{n}=\frac{m+1}{m+n}$ | C. | $\frac{{y}^{2}+y}{xy}=\frac{y+1}{xy}$ | D. | $\frac{a}{b}=\frac{a{c}^{2}}{b{c}^{2}}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖1,⊙O是等邊三角形ABC的外接圓,P是⊙O上的一個點.
如圖1,⊙O是等邊三角形ABC的外接圓,P是⊙O上的一個點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,點O是直線EF上一點,射線OA,OB,OC在直線EF的上方,射線OD的直線EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.
如圖,點O是直線EF上一點,射線OA,OB,OC在直線EF的上方,射線OD的直線EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,長方形紙片ABCD,點E、F分別在邊AB、CD上,連接EF,將∠BEF對折,點B落在直線EF上的B′處,得到折痕EC,將點A落在直線EF上的點A′處,得到折痕EN.
如圖,長方形紙片ABCD,點E、F分別在邊AB、CD上,連接EF,將∠BEF對折,點B落在直線EF上的B′處,得到折痕EC,將點A落在直線EF上的點A′處,得到折痕EN.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com