
【題目】某公司生產(chǎn)某種商品每件成本為20元,這種商品在未來40天內(nèi)的日銷售量y(件)與時間x(天)的關(guān)系如下表:
時間x(天) | 1 | 3 | 6 | 10 | ... |
日銷售量y(件) | 94 | 90 | 84 | 76 | ... |
未來40天內(nèi),前20天每天的價格m(元/件)與時間x(天)的函數(shù)關(guān)系式為![]() (1≤x≤20),后20天每天的價格為30元/件(21≤x≤40).
(1≤x≤20),后20天每天的價格為30元/件(21≤x≤40).
(1)分析上表中的數(shù)據(jù),用所學過的一次函數(shù)、二次函數(shù)、反比例函數(shù)的知識確定一個滿足這些數(shù)據(jù)的y(件)與x(天)之間的函數(shù)關(guān)系式.
(2)當1≤x≤20時,設(shè)日銷售利潤為W元,求出W與x的函數(shù)關(guān)系式.
(3)在未來40天中,哪一天的日銷售利潤最大,最大日銷售利潤是多少?
【答案】(1)y=-2x+96(2)w=![]() (3)第14天時,銷售利潤最大,為578元
(3)第14天時,銷售利潤最大,為578元
【解析】(1)通過觀察表格中的數(shù)據(jù)日銷售量與時間t是均勻減少的,所以確定y與x是一次函數(shù)關(guān)系;(2)利用待定系數(shù)法即可求出函數(shù)關(guān)系式;(3)分前20天和后20天分別討論:根據(jù)日銷售量、每天的價格及時間x可以列出銷售利潤W關(guān)于x的二次函數(shù),然后利用二次函數(shù)的性質(zhì)即可求出哪一天的日銷售利潤最大,最大日銷售利潤是多少.
解:(1)設(shè)一次函數(shù)為y=kx+b,將一次函數(shù)中,得
∴k=2 b=96
∴y=-2x+96
經(jīng)檢驗,其它點的坐標均適合以上解析式,
∴所求函數(shù)解析式為y=-2x+96
(2)設(shè)前20天日銷售利潤為W元
W=(-2x+96)( ![]() x+25-20)
x+25-20)
=![]()
(3)∵前20天日銷售利潤W
∵1≤x≤20
∴當x=14時,W有最大值578(元)
后20天日銷售利潤為S元, ![]()
當21≤x≤40時,S隨x的增大而減小。
∴當x=21時,S有最大值為540元)
∵578>540,
∴第14天時,銷售利潤最大,為578元
“點睛”此題分別考查了一次函數(shù)、二次函數(shù)的應用,解題的關(guān)鍵 首先讀懂題目,正確把握題目的數(shù)量關(guān)系,根據(jù)數(shù)量關(guān)系分別列出函數(shù)關(guān)系式解決問題.


科目:初中數(shù)學 來源: 題型:
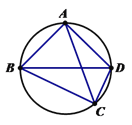
【題目】如圖,點C為△ABD外接圓上的一點(點C不在![]() 上,且不與點B,D重合),且∠ACB=∠ABD=45°,若BC=8,CD=4,則AC的長為( )
上,且不與點B,D重合),且∠ACB=∠ABD=45°,若BC=8,CD=4,則AC的長為( )
A. 8.5 B. ![]() C.
C. 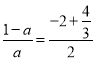 D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,直線![]() 與x軸,y軸分別交于B,C兩點,拋物線
與x軸,y軸分別交于B,C兩點,拋物線![]() 經(jīng)過B,C兩點,點A是拋物線與x軸的另一個交點.
經(jīng)過B,C兩點,點A是拋物線與x軸的另一個交點.

(1)求出點B和點C的坐標.
(2)求此拋物線的函數(shù)解析式.
(3)在拋物線x軸上方存在一點P(不與點C重合),使![]() ,請求出點P的坐標.
,請求出點P的坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】下列因式分解結(jié)果正確的是( )
A.a2﹣9=(a+3)(a﹣3)B.x2﹣x=x(x2﹣1)
C.x2+2x+4=(x+2)2D.﹣4m3+12m2=﹣m2(4m﹣12)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某校九年級“詩歌大會”比賽中,各班代表隊得分如下(單位:分):9,7,8,7,9,7,6,則各代表隊得分的中位數(shù)是______.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在ABCD中,E、F分別是AB、DC邊上的點,且AE=CF, 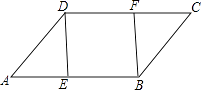
(1)求證:△ADE≌△CBF.
(2)若∠DEB=90°,求證:四邊形DEBF是矩形.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com