
【題目】天封塔歷史悠久,是寧波著名的文化古跡.如圖,從位于天封塔的觀測點C測得兩建筑物底部A,B的俯角分別為45°和60°,若此觀測點離地面的高度為51米,A,B兩點在CD的兩側,且點A,D,B在同一水平直線上,求A,B之間的距離(結果保留根號)
 新編小學單元自測題系列答案
新編小學單元自測題系列答案科目:初中數學 來源: 題型:
【題目】小敏在作⊙O的內接正五邊形時,先做了如下幾個步驟:
(i)作⊙O的兩條互相垂直的直徑,再作OA的垂直平分線交OA于點M,如圖1;
(ii)以M為圓心,BM長為半徑作圓弧,交CA于點D,連結BD,如圖2.若⊙O的半徑為1,則由以上作圖得到的關于正五邊形邊長BD的等式是( )
A.BD2= ![]() OD
OD
B.BD2= ![]() OD
OD
C.BD2= ![]() OD
OD
D.BD2= ![]() OD
OD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】端午節快到了,某市共青團組織以“中學生最喜歡項節日活動”為主題題進行了簡單的隨機抽樣調查,讓學生從“郊外踏青、品嘗美食、觀賞電影、參觀室館”四項活動中選擇一項,然后繪制出以下兩幅不完整的統計圖.請根據圖中的信息,回答下列問題: 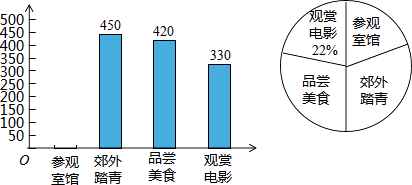
(1)這次抽樣調查中共調查了人;扇形統計圖中郊外踏青部分的圓心角的度數是°;
(2)請補全條形統計圖;
(3)某市有中學生3萬人,請估計選擇郊外踏青的人數有多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列結論正確的是( )
A.x2﹣2是二次二項式
B.單項式﹣x2的系數是1
C.使式子 ![]() 有意義的x的取值范圍是x>﹣2
有意義的x的取值范圍是x>﹣2
D.若分式 ![]() 的值等于0,則a=±1
的值等于0,則a=±1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小剛根據學習“數與式”的經驗,想通過由“特殊到一般”的方法探究下面二次根式的運算規律.
以下是小剛的探究過程,請補充完整;
(1)具體運算,發現規律.
特例1:![]() ;特例2:
;特例2:![]() ;特例3:
;特例3:![]() ;特例4: (舉一個符合上述運算特征的例子)
;特例4: (舉一個符合上述運算特征的例子)
(2)觀察、歸納,得出猜想.
如果n為正整數,用含n的式子表示這個運算規律; .
(3)證明猜想,確認猜想的正確性.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校九年級數學興趣小組的同學調查了若干名家長對“初中學生帶手機上學”現象的看法,統計整理并制作了如下的條形統計圖與扇形統計圖:依據圖中信息,得出下列結論:
(1)接受這次調查的家長人數為200人;
(2)在扇形統計圖中,“不贊同”的家長部分所對應的扇形圓心角大小為162°;
(3)表示“無所謂”的家長人數為40人;
(4)隨機抽查一名接受調查的家長,恰好抽到“很贊同”的家長的概率是 ![]() .
.
其中正確的結論個數為( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一個四邊形的一條對角線把四邊形分成兩個等腰三角形,我們把這條對角線叫這個四邊形的和諧線,這個四邊形叫做和諧四邊形.如菱形就是和諧四邊形.
(1)如圖1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求證:BD是梯形ABCD的和諧線;
(2)如圖2,在12×16的網格圖上(每個小正方形的邊長為1)有一個扇形BAC,點A.B.C均在格點上,請在答題卷給出的兩個網格圖上各找一個點D,使得以A、B、C、D為頂點的四邊形的兩條對角線都是和諧線,并畫出相應的和諧四邊形;
(3)四邊形ABCD中,AB=AD=BC,∠BAD=90°,AC是四邊形ABCD的和諧線,求∠BCD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O的半徑為1,A、P、B、C是⊙O上的四個點,∠APC=∠CPB=60°. 
(1)判斷△ABC的形狀:;
(2)試探究線段PA、PB、PC之間的數量關系,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠C=90°,AC=BC.作射線AP,過點B作BD⊥AP于點D,連接CD.
(1)當射線AP位于圖1所示的位置時
①根據題意補全圖形;
②求證:AD+BD=![]() CD.
CD.
(2)當射線AP繞點A由圖1的位置順時針旋轉至∠BAC的內部,如圖2,直接寫出此時AD,BD,CD三條線段之間的數量關系為 .

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com