
 (1)證明:∵四邊形ABCD是正方形,
(1)證明:∵四邊形ABCD是正方形,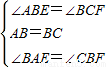
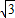 ,…(5分)
,…(5分)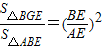 ,
,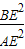 ×S△ABE=
×S△ABE=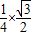 =
=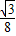 .…(8分)
.…(8分)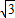 ,BE=1,
,BE=1,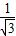 =
=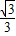 ,∠BAE=30°,…(10分)
,∠BAE=30°,…(10分)

科目:初中數學 來源: 題型:
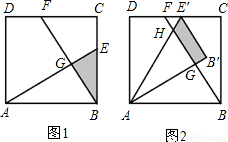
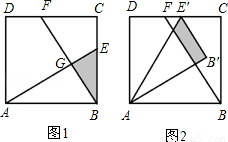
 (2012•益陽)已知:如圖1,在面積為3的正方形ABCD中,E、F分別是BC和CD邊上的兩點,AE⊥BF于點G,且BE=1.
(2012•益陽)已知:如圖1,在面積為3的正方形ABCD中,E、F分別是BC和CD邊上的兩點,AE⊥BF于點G,且BE=1.查看答案和解析>>
科目:初中數學 來源:2012年初中畢業升學考試(湖南益陽卷)數學(帶解析) 題型:解答題
已知:如圖1,在面積為3的正方形ABCD中,E、F分別是BC和CD邊上的兩點,AE⊥BF于點G,且BE=1.
(1)求證:△ABE≌△BCF;
(2)求出△ABE和△BCF重疊部分(即△BEG)的面積;
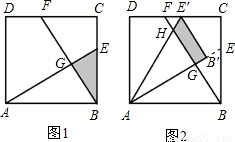
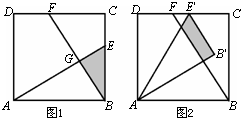
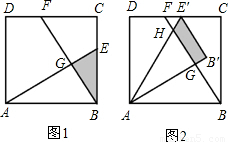
(3)現將△ABE繞點A逆時針方向旋轉到△AB′E′(如圖2),使點E落在CD邊上的點E′處,問△ABE在旋轉前后與△BCF重疊部分的面積是否發生了變化?請說明理由.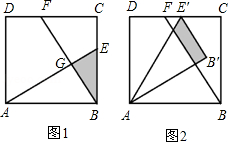
查看答案和解析>>
科目:初中數學 來源:2012年初中畢業升學考試(湖南益陽卷)數學(解析版) 題型:解答題
已知:如圖1,在面積為3的正方形ABCD中,E、F分別是BC和CD邊上的兩點,AE⊥BF于點G,且BE=1.
(1)求證:△ABE≌△BCF;
(2)求出△ABE和△BCF重疊部分(即△BEG)的面積;
(3)現將△ABE繞點A逆時針方向旋轉到△AB′E′(如圖2),使點E落在CD邊上的點E′處,問△ABE在旋轉前后與△BCF重疊部分的面積是否發生了變化?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
已知:如圖1,在面積為3的正方形ABCD中,E、F分別是BC和CD邊上的兩點,AE⊥BF于點G,且BE=1.
(1)求證:△ABE≌△BCF;
(2)求出△ABE和△BCF重疊部分(即△BEG)的面積;
(3)現將△ABE繞點A逆時針方向旋轉到△AB'E'(如圖2),使點E落在CD邊
上的點E'處,問△ABE在旋轉前后與△BCF重疊部分的面積是否發生了變化?請說明理由.
 |
查看答案和解析>>
科目:初中數學 來源:2013年甘肅省武威十三中中考數學模擬試卷(一)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com