
選做題:本題為選做題,從甲、乙兩題中選做一題即可,如果兩題都做,只以甲題計分.
甲題:由山腳下的一點A測得山頂D的仰角是45°,從![]() 沿傾斜角為30°的山坡前進1500米到B,再次測得山頂D的仰角為60°,求山高CD. (結果保留根號)
沿傾斜角為30°的山坡前進1500米到B,再次測得山頂D的仰角為60°,求山高CD. (結果保留根號)
 |
乙題:如圖,Rt△ABO的頂點A是雙曲線![]() 與直線
與直線![]() 在第二象限的交點,AB⊥
在第二象限的交點,AB⊥ 軸于B且S△ABO=
軸于B且S△ABO=![]() .
.

1.求這兩個函數的解析式
2.求直線與雙曲線的兩個交點A、C的坐標,并寫出當x在什么范圍取值時, y.
y.
甲題:過點B作CD,AC的垂線,垂足分別為E,F,
∵∠BAC=30°,AB=1500米,
∴BF=EC=750米.
AF=AB•cos∠BAC=1500×![]() =750
=750![]() 米. (3分)
米. (3分)
設FC=x米,
∵∠DBE=60°,
∴DE=![]() x米.
x米.
又∵∠DAC=45°,
∴AC=CD.
即:750![]() +x=750+
+x=750+![]() x米,
x米,
得x=750. (7分)
∴CD=(750+750![]() 米).(9分)
米).(9分)
答:山高CD為(750+750![]() )米.(10分)
)米.(10分)

乙題:
1.設A點坐標為(x,y),且x<0,y>0,
則S△ABO=12•|BO|•|BA|=12•(-x)•y=32,
∴xy=-3,
又∵y=kx,
即xy=k,
∴k=-3,
∴所求的兩個函數的解析式分別為y=-![]() ,
,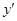 =-x+2;(4分)
=-x+2;(4分)
2.根據題意得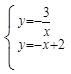 ,解出
,解出 ,得出A(-1,3),C(3,-1);(8分)
,得出A(-1,3),C(3,-1);(8分)
根據圖象可以知道一次函數大于反比例函數的x的取值范圍為x<-1或0<x<3.(10分)
解析:甲題利用三角函數來求解。
乙題(1)欲求這兩個函數的解析式,關鍵求k值.根據反比例函數性質,k絕對值為3且為負數,由此即可求出k;
(2)結合圖象可以知道一次函數大于反比例函數說明一次函數的圖象在反比例函數圖象的上面,由此即可求解。


科目:初中數學 來源: 題型:
| 1 | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 本題為選做題,從甲、乙兩題中選做一題即可,如果兩題都做,只以甲題計分.
本題為選做題,從甲、乙兩題中選做一題即可,如果兩題都做,只以甲題計分.| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| m+2 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•沐川縣二模)本題為選做題,從甲乙兩題中選做一題即可,如果兩題都做,只以甲題計分.
(2012•沐川縣二模)本題為選做題,從甲乙兩題中選做一題即可,如果兩題都做,只以甲題計分.查看答案和解析>>
科目:初中數學 來源: 題型:
 本題為選做題,從甲、乙兩題中選做一題即可,如果兩題都做,只以甲題計分.
本題為選做題,從甲、乙兩題中選做一題即可,如果兩題都做,只以甲題計分.查看答案和解析>>
科目:初中數學 來源:2011-2012學年云南省保山市隆陽區魏家中學九年級(上)第二次月考數學試卷(解析版) 題型:解答題
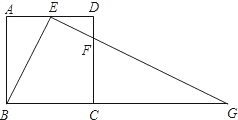
 DC,連接EF并延長交BC的延長線于點G
DC,連接EF并延長交BC的延長線于點G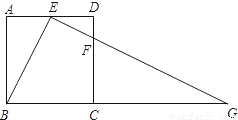
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com