
【題目】青少年視力水平下降已引起全社會的廣泛關注,為了解某市初中畢業年級5 000名學生的視力情況,我們從中抽取了一部分學生的視力作為樣本進行數據處理,得到如下的不完整的頻數分布表和頻數分布直方圖:
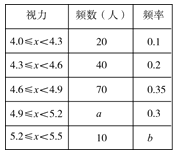
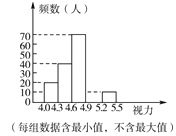
請根據以上圖表信息回答下列問題:
(1)在頻數分布表中,a=________,b=________;
(2)補全條形統計圖;
(3)若視力在4.6以上(含4.6)均屬正常,根據上述信息估計全區初中畢業生中視力正常的學生有多少?
【答案】 60 0.05
【解析】
(1)由頻數分布表中在的信息可知:視力在4.0≤x<4.3的人數為20,頻率為0.1,由此即可得到被抽查的學生總數為:20÷0.1=200(人),這樣由200×0.3可得a,由10÷200可得b;
(2)根據(1)所得a的值,將條形統計圖補充完整即可;
(3)根據題意將視力在4.6及以上的三組數據的頻率相加,再將所得的和與5000相乘即可得到所求的值.
(1)由頻數分布表知,視力在4.0≤x<4.3的人數為20,頻率為0.1,
∴此次調查的總人數為20÷0.1=200,
∴a=200×0.3=60,b=10÷200=0.05;
(2)由(1)可知a=60,則補全條形統計圖如下:
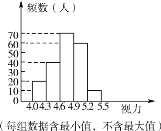
(3)由題意可得:5 000(0.35+0.3+0.05)=3500(人).
答:估計全市九年級學生中視力正常的有3500人.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,A、B、C三點在一條直線上,根據圖形填空:
(1)AC= + + ;
(2)AB=AC﹣ ;
(3)DB+BC= ﹣AD
(4)若AC=8cm,D是線段AC中點,B是線段DC中點,求線段AB的長.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小茗在一張紙上畫一條數軸,并在數軸上標出![]() 、
、![]() 兩個點,點
兩個點,點![]() 表示的數是
表示的數是![]() ,點
,點![]() 表示的數是12.
表示的數是12.
(1)若數軸上點![]() 與點
與點![]() 相距3個單位長度,求點
相距3個單位長度,求點![]() 所表示的數;
所表示的數;
(2)將這張紙對折,使點![]() 與點
與點![]() 剛好重合,折痕與數軸交于點
剛好重合,折痕與數軸交于點![]() ,求點
,求點![]() 表示的數;
表示的數;
(3)點![]() 和點
和點![]() 同時從初始位置沿數軸向左運動,點
同時從初始位置沿數軸向左運動,點![]() 的速度是每秒1個單位長度,點
的速度是每秒1個單位長度,點![]() 的速度是每秒2個單位長度,運動時間是
的速度是每秒2個單位長度,運動時間是![]() 秒.是否存在
秒.是否存在![]() 的值,使
的值,使![]() 秒后點
秒后點![]() 到原點的距離等于點
到原點的距離等于點![]() 到原點的距離的兩倍?若存在,請求出
到原點的距離的兩倍?若存在,請求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】操場上有一根豎直立在地面上的旗桿,繩子自然下垂到地面還剩余2米,當把繩子拉開8米后,繩子剛好斜著拉直下端接觸地面(如圖①)
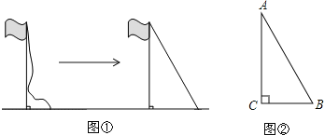
(1)請根據你的閱讀理解,將題目的條件補充完整:如圖②,Rt△ABC中 ∠C=90°,BC=8米,____________________________.求AC的長.
(2)根據(1)中的條件,求出旗桿的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“龜兔首次賽跑”之后,輸了比賽的兔子沒有氣餒,總結反思后,和烏龜約定再賽一場.圖中的函數圖象刻畫了“龜兔再次賽跑”的故事(x表示烏龜從起點出發所行的時間,y1表示烏龜所行的路程,y2表示兔子所行的路程).有下列說法:
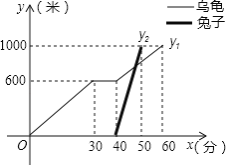
①“龜兔再次賽跑”的路程為1000米;
②兔子和烏龜同時從起點出發;
③烏龜在途中休息了10分鐘;
④兔子在途中750米處追上烏龜.
其中正確的說法是 .(把你認為正確說法的序號都填上)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】模型介紹:古希臘有一個著名的“將軍飲馬問題”,大致內容如下:古希臘一位將軍,每天都要巡查河岸側的兩個軍營A、B,他總是先去A營,再到河邊飲馬,之后再去B營,如圖①,他時常想,怎么走才能使每天的路程之和最短呢?
大數學家海倫曾用軸對稱的方法巧妙的解決了這問題.
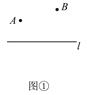
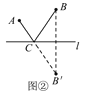
如圖②,作B關于直線l的對稱點B′,連接AB′與直線l交于點C,點C就是所求的位置.
請你在下列的閱讀、應用的過程中,完成解答.
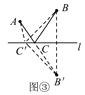
(1)理由:如圖③,在直線l上另取任一點C′,連接AC′,BC′,B′C′,
∵直線l是點B,B′的對稱軸,點C,C′在l上,
∴CB=_______,C′B=_______.
∴AC+CB=AC+CB′=_______.
在△AC′B′中,∵AB′<AC′+C′B′,∴AC+CB<AC′+C′B′,即AC+CB最小.
歸納小結:
本問題實際是利用軸對稱變換的思想,把A、B在直線的同側問題轉化為在直線的兩側,從而可利用“兩點之間線段最短”,即轉化為“三角形兩邊之和大于第三邊”的問題加以解決(其中C為AB′與l的交點,即A、C、B′三點共線).
本問題可拓展為“求定直線上一動點與直線外兩定點的距離和的最小值”問題的數學模型.
(2)模型應用
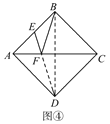
①如圖 ④,正方形ABCD的邊長為2,E為AB的中點,F是AC上一動點,求EF+FB的最小值.
解決這個問題,可以借助上面的模型,由正方形的對稱性可知,B與D關于直線AC對稱,連接ED交AC于F,則EF+FB的最小值就是線段DE的長度,EF+FB的最小值是_______.
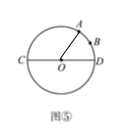
②如圖⑤,已知⊙O的直徑CD為4,∠AOD的度數為60°,點B是弧AD的中點,在直徑CD上找一點P,使BP+AP的值最小,則BP+AP的最小值是_______;
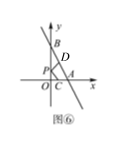
③如圖⑥,一次函數y=-2x+4的圖象與x,y軸分別交于A,B兩點,點O為坐標原點,點C與點D分別為線段OA,AB的中點,點P為OB上一動點,求PC+PD的最小值,并寫出取得最小值時P點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將長為20cm,寬為8cm的長方形白紙,按如圖所示的方式粘合起來,粘合部分的寬為3cm.

(1)根據題意,將下面的表格補充完整.
白紙張數x(張) | 1 | 2 | 3 | 4 | 5 | … |
紙條總長度y(cm) | 20 | 54 | 71 | … |
(2)直接寫出y與x的關系式.
(3)要使粘合后的長方形總面積為1656cm2,則需用多少張這樣的白紙?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數學課本中,有這樣一道題:已知:如(圖1),∠B+∠C=∠BEC求證:AB∥CD
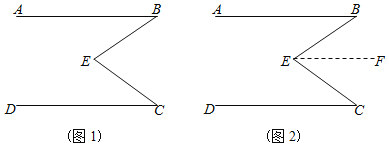
(1)請補充下面證明過程
證明:過點E,做EF∥AB,如(圖2)
∴∠B=∠
∵∠B+∠C=∠BEC∠BEF+∠FEC=∠BEC(已知)
∴∠B+∠C=∠BEF+∠FEC(等量代換)
∴∠ =∠ (等式性質)
∴EF∥
∵EF∥AB
∴AB∥CD(平行于同一條直線的兩條直線互相平行)
(2)請再選用一種方法,加以證明
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com