
如圖,某中學校園有一塊長為35m,寬為16m的長方形空地,其中有一面已經鋪設長為26m的籬笆圍墻,學校設計在這片空地上,利用這面圍墻和用盡已有的可制作50m長的籬笆材料,圍成一個矩形花園或圍成一個半圓花園,請回答以下問題:
(1)能否圍成面積為300m2的矩形花園?若能,請寫出其中一種設計方案,若不能,請說明理由.
(2)若圍成一個半圓花園,則該如何設計?請寫出你的設計方案.(π取3.14)
(3)圍成的各種設計中,最大面積是多少?
(1)能,設計方案見解析;(2)設計方案見解析;(3)343.43m2.
解析試題分析:(1)首先表示出矩形的長與寬,利用矩形面積得出等式,進而解方程得出;
(2)利用已知得出設新增加am,則半圓弧長為: ,進而得出a的值,即可得出答案;
,進而得出a的值,即可得出答案;
(3)利用二次函數最值求法得出矩形最值再利用半圓面積公式得出半圓面積,進而比較即可.
試題解析:(1)設垂直于已經鋪設長為26m的籬笆圍墻的一邊為xm,則平行于原籬笆的長為(50-2x)m,
根據題意得出:x(50-2x)=300,
解得:x1=10,x2=15,
當x=10,則50-20=30>26,故不合題意舍去,
∴能圍成面積為300m2的矩形花園,此時長為20m,寬為15m;
(2)∵當r=13時,∴l半圓=πr=3.14×13=40.82<50,
∴半圓的直徑應大于26m,設新增加am,則半圓弧長為: ,
,
∴a+ =50,
=50,
解得:a≈3.57,
∴半圓直徑為:26+3.57=29.57(m),
∴半圓的半徑為:14.79m;
(3)S1=x(50-2x)=-2x2+50x,
當x=12.5時,S最大= =312.5(m2),
=312.5(m2),
S半圓= π×14.792≈343.43(m2),
π×14.792≈343.43(m2),
∴圍成的各種設計中,最大面積是半圓面積為343.43m2.
考點: 1.二次函數的應用;2.一元二次方程的應用.


科目:初中數學 來源: 題型:解答題
在平面直角坐標系 中,矩形OABC過原點O,且A(0,2)、C(6,0),∠AOC的平分線交AB于點D.
中,矩形OABC過原點O,且A(0,2)、C(6,0),∠AOC的平分線交AB于點D.
(1)直接寫出點B的坐標;
(2)如圖,點P從點O出發,以每秒 個單位長度的速度沿射線OD方向移動;同時點Q從點O出發,以每秒2個單位長度的速度沿
個單位長度的速度沿射線OD方向移動;同時點Q從點O出發,以每秒2個單位長度的速度沿 軸正方向移動.設移動時間為
軸正方向移動.設移動時間為 秒.
秒.
①當t為何值時,△OPQ的面積等于1;
②當t為何值時,△PQB為直角三角形;
(3)已知過O、P、Q三點的拋物線解析式為y=- (x-t)2+t(t>0).問是否存在某一時刻t,將△PQB繞某點旋轉180°后,三個對應頂點恰好都落在上述拋物線上?若存在,求出t的值;若不存在,請說明理由.
(x-t)2+t(t>0).問是否存在某一時刻t,將△PQB繞某點旋轉180°后,三個對應頂點恰好都落在上述拋物線上?若存在,求出t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知直線 分別與y軸、x軸相交于A、B兩點,與二次函數
分別與y軸、x軸相交于A、B兩點,與二次函數 的圖像交于A、C兩點.
的圖像交于A、C兩點.
(1)當點C坐標為( ,
,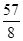 )時,求直線AB的解析式;
)時,求直線AB的解析式;
(2)在(1)中,如圖,將△ABO沿y軸翻折180°,若點B的對應點D恰好落在二次函數 的圖像上,求點D到直線AB的距離;
的圖像上,求點D到直線AB的距離;
(3)當-1≤x≤1時,二次函數 有最小值-3,求實數m的值.
有最小值-3,求實數m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知拋物線 (m是常數,
(m是常數,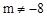 )與x軸有兩個不同的交點A、B,點A、點B關于直線x=1對稱,拋物線的頂點為C.
)與x軸有兩個不同的交點A、B,點A、點B關于直線x=1對稱,拋物線的頂點為C.
(1)此拋物線的解析式;
(2)求點A、B、C的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
在平面直角坐標系xOy中,拋物線 與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C(0,4),D為OC的中點.
與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C(0,4),D為OC的中點.
(1)求m的值;
(2)拋物線的對稱軸與 x軸交于點E,在直線AD上是否存在點F,使得以點A、B、F為頂點的三角形與△ADE 相似?若存在,請求出點F的坐標,若不存在,請說明理由;
(3)在拋物線的對稱軸上是否存在點G,使△GBC中BC邊上的高為 ?若存在,求出點G的坐標;若不存在請說明理由.
?若存在,求出點G的坐標;若不存在請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
某商人如果將進貨價為8元的商品按每件10元出售,每天可銷售100件,現采用提高售出價,減少進貨量的辦法增加利潤,已知這種商品每漲價1元其銷售量就要減少10件,問他將售出價定為多少元時,才能使每天所賺的利潤最大?并求出最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
二次函數 的圖象與x軸交于點A(-1, 0),與y軸交于點C(0,-5),且經過點D(3,-8).
的圖象與x軸交于點A(-1, 0),與y軸交于點C(0,-5),且經過點D(3,-8).
(1)求此二次函數的解析式和頂點坐標;
(2)請你寫出一種平移的方法,使平移后拋物線的頂點落在原點處,并寫出平移后拋物線的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖所示,在平面直角坐標系中,Rt△OBC的兩條直角邊分別落在x軸、y軸上,且OB=1,OC=3,將△OBC繞原點O順時針旋轉90°得到△OAE,將△OBC沿y軸翻折得到△ODC,AE與CD交于點F.
(1)若拋物線過點A、B、C, 求此拋物線的解析式;
(2)求△OAE與△ODC重疊的部分四邊形ODFE的面積;
(3)點M是第三象限內拋物線上的一動點,點M在何處時△AMC的面積最大?最大面積是多少?求出此時點 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知: 為邊長是
為邊長是 的等邊三角形,四邊形
的等邊三角形,四邊形 為邊長是6的正方形. 現將等邊
為邊長是6的正方形. 現將等邊 和正方形
和正方形 按如圖①的方式擺放,使點
按如圖①的方式擺放,使點 與點
與點 重合,點
重合,點 、
、 、
、 在同一條直線上,
在同一條直線上, 從圖①的位置出發,以每秒1個單位長度的速度沿
從圖①的位置出發,以每秒1個單位長度的速度沿 方向向右勻速運動,當點
方向向右勻速運動,當點 與點
與點 重合時暫停運動,設
重合時暫停運動,設 的運動時間為
的運動時間為 秒(
秒( ).
).
(1)在整個運動過程中,設等邊 和正方形
和正方形 重疊部分的面積為
重疊部分的面積為 ,請直接寫出
,請直接寫出 與
與 之間的函數關系式;
之間的函數關系式;
(2)如圖②,當點 與點
與點 重合時,作
重合時,作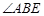 的角平分線
的角平分線 交
交 于點
于點 ,將
,將 繞點
繞點 逆時針旋轉,使邊
逆時針旋轉,使邊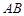 與邊
與邊 重合,得到
重合,得到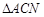 . 在線段
. 在線段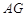 上是否存在
上是否存在 點,使得
點,使得 為等腰三角形. 如果存在,求線段
為等腰三角形. 如果存在,求線段 的長度;若不存在,請說明理由.
的長度;若不存在,請說明理由.
(3)如圖③,若四邊形 為邊長是
為邊長是 的正方形,
的正方形, 的移動速度為每秒
的移動速度為每秒 個單位長度,其余條件保持不變.
個單位長度,其余條件保持不變.  開始移動的同時,
開始移動的同時, 點從
點從 點開始,沿折線
點開始,沿折線 以每秒
以每秒 個單位長度開始移動,
個單位長度開始移動, 停止運動時,
停止運動時, 點也停止運動. 設在運動過程中,
點也停止運動. 設在運動過程中, 交折線
交折線 于
于 點,則當
點,則當 時,求
時,求 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com