等腰三角形一腰上的高與另一腰的夾角為30°,腰長為a,則其底邊上的高是 .
【答案】
分析:題中沒有指明該等腰三角形是銳角三角形還是鈍角三角形,故應該分情況進行分析.
解答:解:顯然三角形不可能為直角三角形,故分兩種情況考慮:
(i)當三角形是銳角三角形時,高與另一腰的夾角為30°,則其頂角是60°,
所以該等腰三角形是等邊三角形,腰是a,則底邊上的高是
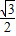
a;
(ii)當三角形是鈍角時,一腰上的高與另一腰的夾角為30°,
則等腰三角形的頂角的外角是60°,因而底角是30°,過頂角頂點作底邊的垂線,則底邊上的高是

a;
所以底邊上的高是
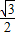
a或

a.
點評:此題考查了等腰三角形的性質及直角三角形的性質的綜合運用.以及分類討論思想.
