
【題目】甲、乙兩位同學做拋骰子(均勻正方體形狀)實驗,他們共拋了60次,出現向上點數的次數如表:
向上點數 | 1 | 2 | 3 | 4 | 5 | 6 |
出現次數 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)計算出現向上點數為6的頻率.
(2)丙說:“如果拋600次,那么出現向上點數為6的次數一定是100次.”請判斷丙的說法是否正確并說明理由.
(3)如果甲乙兩同學各拋一枚骰子,求出現向上點數之和為3的倍數的概率.
【答案】(1)![]() ;(2)丙的說法不正確,理由詳見解析;(3)
;(2)丙的說法不正確,理由詳見解析;(3)![]() .
.
【解析】
(1)用出現6的次數除總次數即可得解;
(2)丙的說法不正確,理由:(1)因為實驗次數較多時,向上點數為![]() 的頻率接近于概率,但不說明概率就等一定等于頻率;(2)從概率角度來說,向上點數為
的頻率接近于概率,但不說明概率就等一定等于頻率;(2)從概率角度來說,向上點數為![]() 的概率是
的概率是![]() 的意義是指平均每
的意義是指平均每![]() 次出現
次出現![]() 次;
次;
(3)根據列出表格,由表格得到所有等結果與點數和為3的倍數的情況,然后根據概率公式求解即可.
解:(1)出現向上點數為![]() 的頻率:
的頻率:![]() ;
;
(2)丙的說法不正確,
理由:(1)因為實驗次數較多時,向上點數為![]() 的頻率接近于概率,但不說明概率就等一定等于頻率;(2)從概率角度來說,向上點數為
的頻率接近于概率,但不說明概率就等一定等于頻率;(2)從概率角度來說,向上點數為![]() 的概率是
的概率是![]() 的意義是指平均每
的意義是指平均每![]() 次出現
次出現![]() 次;
次;
(3)用表格列出所有等可能性結果:
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
共有![]() 種等可能性結果,其中點數之和為
種等可能性結果,其中點數之和為![]() 的倍數可能性結果有
的倍數可能性結果有![]() 個,
個,
∴![]() (點數之和為
(點數之和為![]() 的倍數)
的倍數)![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】商場打折前,買1件A商品和1件B商品用了20元,買30件A商品和40件B商品用了680元.打折后,買100件A商品100件B商品用了1800元.請根據上述信息解決下列問題:
(1)打折前A、B兩種商品的單價分別是多少?
(2)請在(1)的基礎上提出一個能使題目剩余條件解決的問題,并加以解決.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,E、F分別是CD、AB延長線上的點,連結EF,分別交AD、BC于點G、H.若∠1=∠2,∠A=∠C,試說明AD//BC和AB//CD.請完成下面的推理過程,填寫理由或數學式:

∵∠1=∠2,∠1=∠AGH(_________)
∴∠2=∠AGH(________)
∴AD//BC(________)
∴∠ADE=∠C(________)
∵∠A=∠C(已知)
∴∠ADE=_______(等量代換)
∴AB//CD(_______)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學課上,老師出了一道題:化簡
[8(a+b)5-4(a+b)4+(-a-b)3]÷[2(a+b)3].
小明同學馬上舉手,下面是小明的解題過程:
[8(a+b)5-4(a+b)4+(-a-b)3]÷[2(a+b)3]
=[8(a+b)5-4(a+b)4+(a+b)3]÷8(a+b)3
=(a+b)2-![]() (a+b)+
(a+b)+ ![]() .
.
小亮也舉起了手,說小明的解題過程不對,并指了出來.老師肯定了小亮的回答.你知道小明錯在哪兒嗎?請指出來,并寫出正確解答.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC=10,BC=12,點D在邊BC上,且BD=4,以點D為頂點作∠EDF=∠B,分別交邊AB于點E,交AC或延長線于點F. 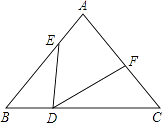
(1)當AE=4時,求AF的長;
(2)當以邊AC為直徑的⊙O與線段DE相切時,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著互聯網、移動終端的迅速發展,數字化閱讀越來越普及,公交上的“低頭族”越來越多.某研究機構針對“您如何看待數字化閱讀”問題進行了隨機問卷調查(如圖1),并將調查結果繪制成圖2和圖3所示的統計圖(均不完整).請根據統計圖中提供的信息,解答下列問題: 
(1)求出本次接受調查的總人數,并將條形統計圖補充完整;
(2)表示觀點B的扇形的圓心角度數為度;
(3)2016年底慈溪人口總數約為200萬(含外來務工人員),請根據圖中信息,估計慈溪市民認同觀點D的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=8,BC=10,以B為圓心,任意長為半徑畫弧分別交BA、BC于點M和N,再分別以M、N為圓心,大于 ![]() MN長為半徑畫弧,兩弧交于點P,連結BP并延長交AC于點D,若△BDC的面積為20,則△ABD的面積為( )
MN長為半徑畫弧,兩弧交于點P,連結BP并延長交AC于點D,若△BDC的面積為20,則△ABD的面積為( ) 
A.20
B.18
C.16
D.12
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com