解:(1)解方程x
2-4x+3=0得:
x=1或x=3,而OA<OB,
則點A的坐標為(-1,0),點B的坐標為(3,0);
∵A、B關于拋物線對稱軸對稱,
∴△DAB是等腰三角形,而∠DAB=45°,
∴△DAB是等腰直角三角形,得D(1,-2);
令拋物線對應的二次函數(shù)解析式為y=a(x-1)
2-2,
∵拋物線過點A(-1,0),
∴0=4a-2,得a=

,
故拋物線對應的二次函數(shù)解析式為y=

(x-1)
2-2(或寫成y=

x
2-x-

);
(2)∵CA⊥AD,∠DAC=90°,
又∵∠DAB=45°,
∴∠CAB=45°;
令點C的坐標為(m,n),則有m+1=n,
∵點C在拋物線上,
∴n=

(m-1)
2-2;
化簡得m
2-4m-5=0
解得m=5,m=-1(舍去),
故點C的坐標為(5,6);

(3)由(2)知AC=6

,而AD=2

,
∴DC=
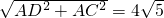
;
過A作AM⊥CD,
又∵
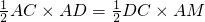
,
∴AM=
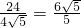
,
又∵S
△ADC=S
△APD+S
△APC∴
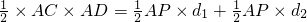
,
d
1+d
2=
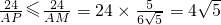
;
即此時d
1+d
2的最大值為4

.
分析:(1)通過解方程即可求得OA、OB的長,從而得到點A、B的坐標,由于A、B關于拋物線的對稱軸對稱,且∠DAB=45°,那么△DAB是等腰直角三角形,即可利用點A、B的坐標求得點D的坐標,然后根據(jù)待定系數(shù)法求得拋物線的解析式;
(2)由于AC⊥AD,且∠DAB=45°,則∠CAB=45°,設出點C的橫坐標,那么其縱坐標應為m+1,然后將C點坐標代入拋物線的解析式中,即可求得點C的坐標;
(3)易得AC、AD的長,由于△ACD是直角三角形,那么AC•AD=AP•d
1+AP•d
2,由此可得d
1+d
2=
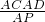
,過A作AM⊥CD于M,利用△ACD的面積可求得AM的長,在Rt△APM中,AP≥AM,故d
1+d
2≤
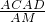
,而AC、AD、AM的長都已求得,由此可確定d
1+d
2的最大值.
點評:此題主要考查了等腰直角三角形的性質、二次函數(shù)解析式的確定、函數(shù)圖象交點坐標的求法、三角形面積的計算方法以及不等式的應用等重要知識,涉及知識面廣,難度較大.

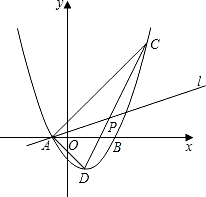 頂點,O為坐標原點.若OA、OB(OA<OB)的長分別是方程x2-4x+3=0的兩根,且∠DAB=45°.
頂點,O為坐標原點.若OA、OB(OA<OB)的長分別是方程x2-4x+3=0的兩根,且∠DAB=45°. ,
, (x-1)2-2(或寫成y=
(x-1)2-2(或寫成y= x2-x-
x2-x- );
); (m-1)2-2;
(m-1)2-2;
 ,而AD=2
,而AD=2 ,
,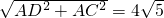 ;
;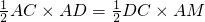 ,
,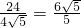 ,
,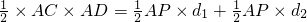 ,
,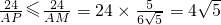 ;
; .
.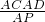 ,過A作AM⊥CD于M,利用△ACD的面積可求得AM的長,在Rt△APM中,AP≥AM,故d1+d2≤
,過A作AM⊥CD于M,利用△ACD的面積可求得AM的長,在Rt△APM中,AP≥AM,故d1+d2≤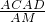 ,而AC、AD、AM的長都已求得,由此可確定d1+d2的最大值.
,而AC、AD、AM的長都已求得,由此可確定d1+d2的最大值.

 閱讀快車系列答案
閱讀快車系列答案 如圖,在平面直角坐標中,四邊形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,點P為x軸上的一個動點,但是點P不與點0、點A重合.連接CP,D點是線段AB上一點,連接PD.
如圖,在平面直角坐標中,四邊形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,點P為x軸上的一個動點,但是點P不與點0、點A重合.連接CP,D點是線段AB上一點,連接PD. (2012•渝北區(qū)一模)如圖,在平面直角坐標xoy中,以坐標原點O為圓心,3為半徑畫圓,從此圓內(包括邊界)的所有整數(shù)點(橫、縱坐標均為整數(shù))中任意選取一個點,其橫、縱坐標之和為0的概率是
(2012•渝北區(qū)一模)如圖,在平面直角坐標xoy中,以坐標原點O為圓心,3為半徑畫圓,從此圓內(包括邊界)的所有整數(shù)點(橫、縱坐標均為整數(shù))中任意選取一個點,其橫、縱坐標之和為0的概率是 如圖,在平面直角坐標xOy中,已知點A(-5,0),P是反比例函數(shù)y=
如圖,在平面直角坐標xOy中,已知點A(-5,0),P是反比例函數(shù)y= ∠COA=45°,動點P從點O出發(fā),在梯形OABC的邊上運動,路徑為O→A→B→C,到達點C時停止.作直線CP.
∠COA=45°,動點P從點O出發(fā),在梯形OABC的邊上運動,路徑為O→A→B→C,到達點C時停止.作直線CP.