
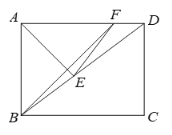
【題目】如圖,在矩形ABCD中,AB=6,BC=8,點E是對角線BD上的一點,把△ABE沿著直線AE翻折得到△AFE,且點F恰好落在AD邊上,連接BF.
(1)求△DEF的周長;
(2)求sin∠BFE的值.
【答案】(1)12;(2)![]()
【解析】
解法一:(1)首先根據矩形的性質和勾股定理得出BD的長度,然后由折疊的性質得出![]() ,則
,則![]() 的周長為
的周長為![]() ,代入相應的數值即可計算;
,代入相應的數值即可計算;
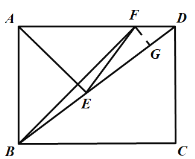
(2)作![]() 于點
于點![]() ,首先由
,首先由![]() 得出
得出![]() ,然后利用
,然后利用![]() 求出FG的長度,利用勾股定理求出BF的長度,則
求出FG的長度,利用勾股定理求出BF的長度,則![]() ,則答案可求;
,則答案可求;
解法二:(1)首先根據矩形的性質和勾股定理得出BD的長度,然后由折疊的性質得出![]() ,則
,則![]() 的周長為
的周長為![]() ,代入相應的數值即可計算;
,代入相應的數值即可計算;
(2)延長![]() 交
交![]() 于點
于點![]() ,首先軸對稱性質可得
,首先軸對稱性質可得![]() ,進而得出
,進而得出![]() 為等腰直角三角形,然后利用
為等腰直角三角形,然后利用![]() 得出
得出![]() ,進而求出BE,EF的長度,然后利用勾股定理求出BF的長度,進而求出FN的長度,再利用勾股定理求出EN的長度,最后利用
,進而求出BE,EF的長度,然后利用勾股定理求出BF的長度,進而求出FN的長度,再利用勾股定理求出EN的長度,最后利用![]() 即可求解.
即可求解.
解法一: ![]() 四邊形
四邊形![]() 是矩形,
是矩形,
![]() .
.
在![]() 中,
中,![]() ,
,
由勾股定理得![]() .
.
由軸對稱性質可得![]() ,
,
![]() ,
,
![]() 的周長
的周長![]() ;
;
![]() 作
作![]() 于點
于點![]() ,
,
![]()
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
解得![]() .
.
在![]() 中,
中,![]() ,由勾股定理得
,由勾股定理得![]() .
.
在![]() 中,
中,
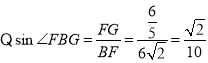 ,
,
![]() .
.
解法二:![]() 同解法一;
同解法一;
![]() 如圖2,延長
如圖2,延長![]() 交
交![]() 于點
于點![]() ,記
,記![]() 的交點為
的交點為![]() ,
,

由軸對稱性質可得![]() ,
,
又![]() ,
,
![]() 為等腰直角三角形,且
為等腰直角三角形,且![]() ,
,
![]()
![]() ,
,
![]() ,
,
即![]() ,
,
解得![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,
由勾股定理得![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,
由勾股定理得![]() ,
,
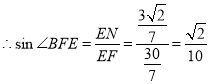 .
.


科目:初中數學 來源: 題型:
【題目】某校為調查“停課不停學”期間九年級學生平均每天上網課時長,隨機抽取了![]() 名九年級學生做網絡問卷調查.共四個選項:
名九年級學生做網絡問卷調查.共四個選項:![]() 小時以下)、
小時以下)、![]() 小時)、
小時)、![]() 小時),
小時), ![]() 小時以上),每人只能選一
小時以上),每人只能選一
項.并將調查結果繪制成如下不完整的統計表和統計圖.
被調查學生平均每天上網課時間統計表
時長 | 所占百分比 |
|
|
|
|
|
|
|
|
合計 |
|
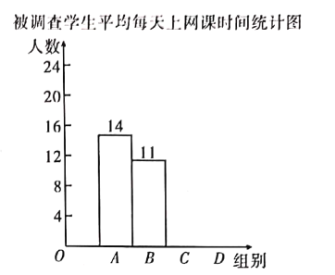
根據以上信息,解答下列問題:
![]() ,
,![]() ,
,
![]() 補全條形統計圖;
補全條形統計圖;
![]() 該校有九年級學生
該校有九年級學生![]() 名,請你估計仝校九年級學生平均每天上網課時長在
名,請你估計仝校九年級學生平均每天上網課時長在![]() 小時及以上的共多少名;
小時及以上的共多少名;
![]() 在被調查的對象中,平均每天觀看時長超過
在被調查的對象中,平均每天觀看時長超過![]() 小時的,有
小時的,有![]() 名來自九
名來自九![]() 班,
班,![]() 名來自九
名來自九![]() 班,其余都來自九
班,其余都來自九![]() 班,現教導處準備從
班,現教導處準備從![]() 選項中任選兩名學生進行電話訪談,請用列表法或畫樹狀圖的方法求所抽取的
選項中任選兩名學生進行電話訪談,請用列表法或畫樹狀圖的方法求所抽取的![]() 名學生恰好來自同一個班級的概率.
名學生恰好來自同一個班級的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,AB=4,BC=5,∠ABC=60°. 按以下步驟作圖:①以C為圓心,以適當長為半徑做弧,交CB、CD于M、N兩點;②分別以M、N為圓心,以大于![]() MN的長為半徑作弧,兩弧相交于點E,作射線CE交BD于點O,交AD邊于點F;則BO的長度為( )
MN的長為半徑作弧,兩弧相交于點E,作射線CE交BD于點O,交AD邊于點F;則BO的長度為( )
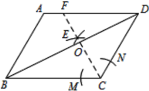
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2020年3月20日,深圳市民中心及周邊樓宇為當日返回深圳的援鄂醫療隊員亮燈,歡迎最美逆行者回家.小洪在歡迎英雄回家現場,如圖,若他觀測到英雄畫像電子屏頂端A和底端C的仰角分別為∠α和∠β,小洪所站位置E到電子屏邊緣AC垂直地面的B點距離為m米,那么英雄畫像電子屏高AC為( )
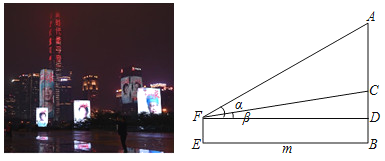
A.![]() 米B.mtan(α﹣β)米
米B.mtan(α﹣β)米
C.m(tanα﹣tanβ)米D.![]() 米
米
查看答案和解析>>
科目:初中數學 來源: 題型:
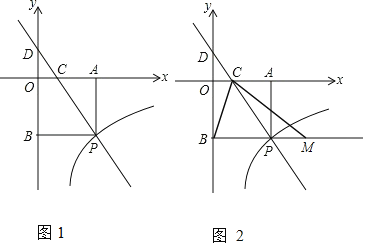
【題目】如圖1,直線y1=kx+3與雙曲線![]() (x>0)交于點P,PA⊥x軸于點A,PB⊥y軸于點B,直線y1=kx+3分別交x軸、y軸于點C和點D,且S△DBP=27,
(x>0)交于點P,PA⊥x軸于點A,PB⊥y軸于點B,直線y1=kx+3分別交x軸、y軸于點C和點D,且S△DBP=27,![]() .
.
(1)求OD和AP的長;
(2)求m的值;
(3)如圖2,點M為直線BP上的一個動點,連接CB、CM,當△BCM為等腰三角形時,請直接寫出點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】PM2.5是指大氣中直徑小于或等于2.5μm(0.0000025m)的顆粒物,含有大量有毒、有害物質,也稱可入肺顆粒物.將0.0000025用科學記數法表示為
A.25×10﹣7B.2.5×10﹣6C.0.25×10﹣5D.2.5×106
查看答案和解析>>
科目:初中數學 來源: 題型:
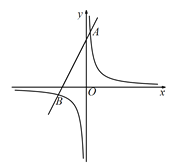
【題目】如圖,在平面系中,一次函數![]() 的圖像經過定點A,反比例函數
的圖像經過定點A,反比例函數![]() 的圖像經過點A,且與一次函數
的圖像經過點A,且與一次函數![]() 的圖像相交于點B(
的圖像相交于點B(![]() ,m).
,m).
(1)求m、a的值;
(2)設橫坐標為n的點P在反比例函數圖象的第三象限上,且在點B右側,連接AP、BP,△ABP的面積為12,求代數式![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有兩張完全重合的矩形紙片,將其中一張繞點![]() 順時針旋轉
順時針旋轉![]() 后得到矩形
后得到矩形![]() (如圖1),連接
(如圖1),連接![]() ,
,![]() ,若
,若![]() ,
,![]() .
.

(1)試探究線段![]() 與線段
與線段![]() 的數量關系和位置關系,并說明理由;
的數量關系和位置關系,并說明理由;
(2)把![]() 與
與![]() 剪去,將
剪去,將![]() 繞點
繞點![]() 順時針旋轉得
順時針旋轉得![]() ,邊
,邊![]() 交
交![]() 于點
于點![]() (如圖2),設旋轉角為
(如圖2),設旋轉角為![]() ,當
,當![]() 為等腰三角形時,求
為等腰三角形時,求![]() 的度數;
的度數;
(3)若將![]() 沿
沿![]() 方向平移得到
方向平移得到![]() (如圖3),
(如圖3),![]() 與
與![]() 交于點
交于點![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,當
,當![]() 時,求平移的距離.
時,求平移的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com