
【題目】已知:如圖,⊙A與y軸交于C、D兩點,圓心A的坐標為(1,0),⊙A的半徑為![]() ,過點C作⊙A的切線交x軸于點B(-4,0).
,過點C作⊙A的切線交x軸于點B(-4,0).
(1)求切線BC的解析式;
(2)若點P是第一象限內⊙A上的一點,過點P作⊙A的切線與直線BC相交于點G,且∠CGP=120°,求點G的坐標.

【答案】(1)![]() ;(2)G(
;(2)G(![]() ,
,![]() +2 ).
+2 ).
【解析】
(1)連接AC,由于BC與⊙A相切,則AC⊥BC,在Rt△ABC中,OC⊥AB,根據射影定理即可求得OC的長,從而得到C點的坐標,進而用待定系數法求出直線BC的解析式.
(2)可設出G點的坐標(設橫坐標,利用直線BC的解析式表示縱坐標),連接AP、AG;由于GC、GP都是⊙A的切線,那么∠AGC=∠ABP=60°,在Rt△AGC中,AC的長易求得,根據∠AGC的度數,即可求得AG的長;過G作GH⊥x軸于H,在Rt△GAH中,可根據G點的坐標表示出AH、GH的長,進而由勾股定理求得G點的坐標.
解:(1)如圖1所示,連接AC,則AC=![]() .
.
在Rt△AOC中,AC=![]() ,OA=1,則OC=2,
,OA=1,則OC=2,
∴點C的坐標為(0,2).
設切線BC的解析式為y=kx+b,
它過點C(0,2),B(﹣4,0),
則有![]() ,
,
解之得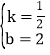 ,
,
∴![]() ;
;
(2)如圖1所示,設點G的坐標為(a,c),
∵點G在直線y=![]() x+2上,
x+2上,
∴c=![]() a+2,
a+2,
過點G作GH⊥x軸,垂足為H點,則OH=a,GH=c=![]() a+2,連接AP,AG.
a+2,連接AP,AG.
∵AC=AP,AG=AG,所以Rt△ACG≌Rt△APG (HL),
∴∠AGC=![]() ×120°=60°.
×120°=60°.
在Rt△ACG中,
∵∠AGC=60°,AC=![]() ,
,
∴sin60°=![]() ,
,
∴AG=![]() .
.
在Rt△AGH中,AH=OH﹣OA=a﹣1,GH=![]() a+2,
a+2,
∵AH2+GH2=AG2,
∴(a﹣1)2+![]() =
=![]() ,
,
解之得:a1=![]() ,a2=﹣
,a2=﹣![]() (舍去),
(舍去),
點G的坐標為(![]() ,
,![]() +2 ).
+2 ).


 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案科目:初中數學 來源: 題型:
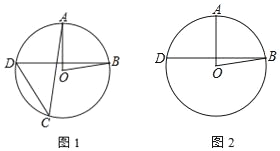
【題目】如圖,在⊙O中,半徑OA與弦BD垂直,點C在⊙O上,∠AOB=80°
(1)若點C在優弧BD上,求∠ACD的大小;
(2)若點C在劣弧BD上,直接寫出∠ACD的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
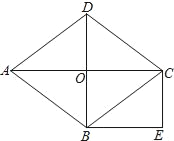
【題目】如圖,O是菱形ABCD對角線AC與BD的交點,CD=5cm,OD=3cm;過點C作CE∥DB,過點B作BE∥AC,CE與BE相交于點E.
(1)求OC的長;
(2)求四邊形OBEC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知等腰三角形ABC的底角為30°,以BC為直徑的⊙O與底邊AB交于點D,過D作DE⊥AC,垂足為E.
(1)證明:DE為⊙O的切線;
(2)若BC=4,求陰影部分的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
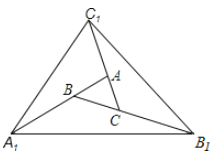
【題目】如圖,對面積為S的△ABC逐次進行以下操作:第一次操作,分別延長AB、BC、CA至點A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,順次連接A1、B1、C1,得到△A1B1C1,記其面積為S1;第二次操作,分別延長A1B1、B1C1、C1A1至點A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,順次連接A2、B2、C2,得到△A2B2C2,記其面積為S2;··· ;則![]() ______. 按此規律繼續下去,可得到
______. 按此規律繼續下去,可得到![]() ,則其面積
,則其面積![]() _______.
_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A,B,C都在拋物線y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x軸,∠ABC=135°,且AB=4.
<a<0)上,AB∥x軸,∠ABC=135°,且AB=4.
(1)填空:拋物線的頂點坐標為 (用含m的代數式表示);
(2)求△ABC的面積(用含a的代數式表示);
(3)若△ABC的面積為2,當2m﹣5≤x≤2m﹣2時,y的最大值為2,求m的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
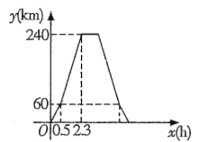
【題目】一輛快遞車從長春出發,走高速公路,途經伊通,前往靖宇鎮送快遞,到達后卸貨和休息共用![]() ,然后開車按原速原路返回長春.這輛快遞車在長春到伊通、伊通到靖宇的路段上分別以不同的速度保持勻速前進,返回時也分別按原速返回.這輛快遞車距離長春的路程
,然后開車按原速原路返回長春.這輛快遞車在長春到伊通、伊通到靖宇的路段上分別以不同的速度保持勻速前進,返回時也分別按原速返回.這輛快遞車距離長春的路程![]() 與它行駛的時間
與它行駛的時間![]() 之間的函數圖象如圖所示.
之間的函數圖象如圖所示.
(1)快遞車從伊通到長春的速度是__________![]() ,快遞車從長春到靖宇鎮往返一共用了__________
,快遞車從長春到靖宇鎮往返一共用了__________![]() ;
;
(2)當這輛快遞車在靖宇到伊通的路段上行駛時,求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(3)如果這輛快遞車兩次經過同一個服務區的時間間隔為![]() ,直接寫出這個服務區距離伊通的路程.
,直接寫出這個服務區距離伊通的路程.
查看答案和解析>>
科目:初中數學 來源: 題型:
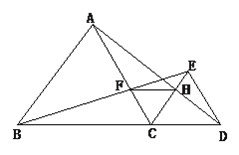
【題目】如圖,已知點B、C、D在同一條直線上,△ABC和△CDE都是等邊三角形.BE交AC于F,AD交CE于H,
①求證:△BCE≌△ACD;
②求證:CF=CH;
③判斷△CFH的形狀并說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=CB,O是AB的中點,CA與⊙O相切于點E,CO交⊙O于點D
(1)求證:CB是⊙O的切線;
(2)若∠ACB=80°,點P是⊙O上一個動點(不與D,E兩點重合),求∠DPE的度數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com