
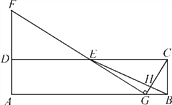
【題目】如圖,在矩形ABCD中,E為CD的中點(diǎn),H為BE上的一點(diǎn), ![]() =3,連接CH并延長(zhǎng)交AB于點(diǎn)G,連接GE并延長(zhǎng)交AD的延長(zhǎng)線(xiàn)于點(diǎn)F.
=3,連接CH并延長(zhǎng)交AB于點(diǎn)G,連接GE并延長(zhǎng)交AD的延長(zhǎng)線(xiàn)于點(diǎn)F.
(1)求證: ![]() ;
;
(2)若∠CGF=90°,求![]() 的值.
的值.
【答案】(1)證明見(jiàn)解析;(2) ![]() =3
=3![]() .
.
【解析】試題分析:(1)根據(jù)相似三角形判定的方法,判斷出△CEH∽△GBH,即可推得結(jié)論;
(2)作EM⊥AB于M,則EM=BC=AD,AM=DE,設(shè)DE=CE=3a,則AB=CD=6a,由(1)得: ![]() =3,得出BG=
=3,得出BG=![]() CE=a,AG=5a,證明△DEF∽△GEC,由相似三角形的性質(zhì)得出EGEF=DEEC,由平行線(xiàn)證出
CE=a,AG=5a,證明△DEF∽△GEC,由相似三角形的性質(zhì)得出EGEF=DEEC,由平行線(xiàn)證出![]() =
=![]() ,得出EF=
,得出EF=![]() EG,求出EG=
EG,求出EG=![]() a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM=
a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM=![]() a,即可得出結(jié)果.
a,即可得出結(jié)果.
試題解析:解:(1)∵四邊形ABCD是矩形,∴CD∥AB,AD=BC,AB=CD,AD∥BC,∴△CEH∽△GBH,∴ ![]() .
.
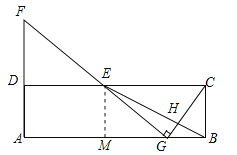
(2)作EM⊥AB于M,如圖所示:
則EM=BC=AD,AM=DE,∵E為CD的中點(diǎn),∴DE=CE,設(shè)DE=CE=3a,則AB=CD=6a,由(1)得: ![]() =3,∴BG=
=3,∴BG=![]() CE=a,∴AG=5a,∵∠EDF=90°=∠CGF,∠DEF=∠GEC,∴△DEF∽△GEC,∴
CE=a,∴AG=5a,∵∠EDF=90°=∠CGF,∠DEF=∠GEC,∴△DEF∽△GEC,∴![]() ,∴EGEF=DEEC,∵CD∥AB,∴
,∴EGEF=DEEC,∵CD∥AB,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴EF=
,∴EF=![]() EG,∴EG
EG,∴EG![]() EG=3a3a,解得:EG=
EG=3a3a,解得:EG=![]() a,在Rt△EMG中,GM=2a,∴EM=
a,在Rt△EMG中,GM=2a,∴EM=![]() =
=![]() a,∴BC=
a,∴BC=![]() a,∴
a,∴![]() =
=![]() =
=![]() .
.


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
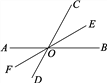
【題目】如圖,直線(xiàn)AB、CD相交于點(diǎn)O,OE平分∠BOC,∠BOC=70°,OF是OE的反向延長(zhǎng)線(xiàn).
(1)求∠DOF與∠BOF的度數(shù);
(2)OF平分∠AOD嗎?為什么?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,點(diǎn)O為坐標(biāo)原點(diǎn),直線(xiàn)y=﹣x+b與坐標(biāo)軸交于C,D兩點(diǎn),直線(xiàn)AB與坐標(biāo)軸交于A(yíng),B兩點(diǎn),線(xiàn)段OA,OC的長(zhǎng)是方程x2﹣3x+2=0的兩個(gè)根(OA>OC).
(1)求點(diǎn)A,C的坐標(biāo);
(2)直線(xiàn)AB與直線(xiàn)CD交于點(diǎn)E,若點(diǎn)E是線(xiàn)段AB的中點(diǎn),反比例函數(shù)y=![]() (k≠0)的圖象的一個(gè)分支經(jīng)過(guò)點(diǎn)E,求k的值;
(k≠0)的圖象的一個(gè)分支經(jīng)過(guò)點(diǎn)E,求k的值;
(3)在(2)的條件下,點(diǎn)M在直線(xiàn)CD上,坐標(biāo)平面內(nèi)是否存在點(diǎn)N,使以點(diǎn)B,E,M,N為頂點(diǎn)的四邊形是菱形?若存在,請(qǐng)直接寫(xiě)出滿(mǎn)足條件的點(diǎn)N的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】巴黎與北京的時(shí)差為﹣7小時(shí)(正數(shù)表示同一時(shí)刻比北京時(shí)間早的時(shí)數(shù)),如果北京時(shí)間11月11日14:00,那么巴黎時(shí)間是( )
A.11月11日21時(shí)
B.11月11日7時(shí)
C.11月10日7時(shí)
D.11月11日5時(shí)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,O是矩形ABCD的對(duì)角線(xiàn)的交點(diǎn),作DE∥AC,CE∥BD,DE、CE相交于點(diǎn)E.求證: 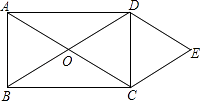
(1)四邊形OCED是菱形.
(2)連接OE,若AD=4,CD=3,求菱形OCED的周長(zhǎng)和面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
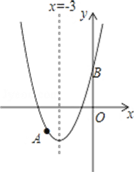
【題目】如圖,拋物線(xiàn)y=x2+bx+c過(guò)點(diǎn)A(﹣4,﹣3),與y軸交于點(diǎn)B,對(duì)稱(chēng)軸是x=﹣3,請(qǐng)解答下列問(wèn)題:
(1)求拋物線(xiàn)的解析式.
(2)若和x軸平行的直線(xiàn)與拋物線(xiàn)交于C,D兩點(diǎn),點(diǎn)C在對(duì)稱(chēng)軸左側(cè),且CD=8,求△BCD的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,矩形ABCD的邊BC與x軸重合,連接對(duì)角線(xiàn)BD交y軸于點(diǎn)E,過(guò)點(diǎn)A作AG⊥BD于點(diǎn)G,直線(xiàn)GF交AD于點(diǎn)F,AB、OC的長(zhǎng)分別是一元二次方程x-5x+6=0的兩根(AB>OC),且tan∠ADB=![]() .
.
(1)求點(diǎn)E、點(diǎn)G的坐標(biāo);
(2)直線(xiàn)GF分△AGD為△AGF與△DGF兩個(gè)三角形,且S△AGF:S△DGF =3:1,求直線(xiàn)GF的解析式;
(3)點(diǎn)P在y軸上,在坐標(biāo)平面內(nèi)是否存在一點(diǎn)Q,使以點(diǎn)B、D、P、Q為頂點(diǎn)的四邊形是矩形?若存在,請(qǐng)直接寫(xiě)出點(diǎn)Q的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
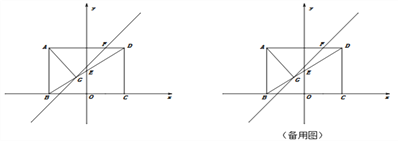
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某工廠(chǎng)有甲種原料360kg,乙種原料290kg,計(jì)劃用這兩種原料生產(chǎn)A、B兩種產(chǎn)品共50件,已知生產(chǎn)一件A種產(chǎn)品,需用甲種原料9kg,乙種原料3kg,可獲利潤(rùn)700元;生產(chǎn)一件B種產(chǎn)品,需用甲種原料4kg,乙種原料10kg,可獲利潤(rùn)1200元.
(1)按要求安排A、B兩種產(chǎn)品的生產(chǎn)件數(shù),有哪幾種方案?請(qǐng)你設(shè)計(jì)出來(lái);
(2)設(shè)生產(chǎn)A、B兩種產(chǎn)品總利潤(rùn)是W(元),采用哪種生產(chǎn)方案獲總利潤(rùn)最大?最大利潤(rùn)為多少?
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com