
【題目】已知,如圖,在△ABC中,AB=AC,∠ABC=∠ACB,D是AB的中點,DE⊥AB交AC于E,若∠BEC=∠C.

(1)若BE平分∠ABC,求∠A的度數;
(2)若△ABC的周長為10,△BCE的周長為6,求BC的長度。
【答案】(1)36°;(2)2.
【解析】
(1)設∠A的度數為x,根據等腰三角形的性質和線段垂直平分線的性質用x表示出∠ABC和∠C,根據三角形內角和定理列出算式求出x的值即可;
(2)根據線段垂直平分線的性質和三角形周長公式計算即可.
(1)設∠A的度數為x,
∵D是AB的中點,DE⊥AB,
∴EA=EB,
∴∠ABE=∠A=x,
∵BE平分∠ABC,
∴∠ABE=∠CBE=x,
∵∠BEC=∠ABE+∠A=2x,
∴∠C=2x,
∴x+2x+2x=180°,
∴∠A=x=36°;
(2)∵△ABC的周長為10,
∴AB+AC+BC=10,
∵△BCE的周長為6,
∴BE+EC+BC=6,即AC+BC=6,
∴AB=4,
則BC=2.


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
【題目】在學校的社會實踐活動中,一批學生協助搬運初一、二兩個年級的圖書,初一年級需要搬運的圖書數量是初二年級需要搬運的圖書數量的兩倍.上午全部學生在初一年級搬運,下午一半的學生仍然留在初一年級(上下午的搬運時間相等)搬運,到放學時剛好把初一年級的圖書搬運完.下午另一半的學生去初二年級搬運圖書,到放學時還剩下一小部分未搬運,最后由三個學生再用一整天的時間剛好搬運完.如果這批學生每人每天搬運的效率是相同的,則這批學生共有人數為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形![]() ,對角線
,對角線![]() 的中點為
的中點為![]() ,點
,點![]() 同時是正方形
同時是正方形![]() 的一個頂點,
的一個頂點,![]() 交
交![]() 于點
于點![]() ,
,![]() 交
交![]() 于點
于點![]() ,若這兩個正方形的邊長都是3,將正方形
,若這兩個正方形的邊長都是3,將正方形![]() 繞點
繞點![]() 轉動.
轉動.

(1)兩個正方形重疊部分的面積________改變(填“會”或“不會”)
(2)兩個正方形重疊部分的面積若改變,說明理由;若不改變,直接寫出重疊部分的面積.請將答案寫在橫線上________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根的判別式內容:
△=b2﹣4ac>0一元二次方程_____;
△=b2﹣4ac=0一元二次方程_____;
此時方程的兩個根為x1=x2=_____.
△=b2﹣4ac<0一元二次方程_____.
△=b2﹣4ac≥0一元二次方程_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小文同學統計了某小區部分居民每周使用共享單車的時間,并繪制了統計圖,如圖所示.下面有四個推斷:
①小文此次一共調查了![]() 位小區居民
位小區居民
②每周使用時間不足![]() 分鐘的人數多于
分鐘的人數多于![]() 分鐘的人數
分鐘的人數
③每周使用時間超過![]() 分鐘的人數超過調查總人數的一半
分鐘的人數超過調查總人數的一半
④每周使用時間在![]() 分鐘的人數最多
分鐘的人數最多
根據圖中信息,上述說法中正確的是( )

A.①④B.①③C.②③D.②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在路燈下,小明的身高如圖中線段AB所示,他在地面上的影子如圖中線段AC所示,小亮的身高如圖中線段FG所示,路燈燈泡在線段DE上.

(1)請你確定燈泡所在的位置,并畫出小亮在燈光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子長AC=1.4m,且他到路燈的距離AD=2.1m,求燈泡的高.
查看答案和解析>>
科目:初中數學 來源: 題型:
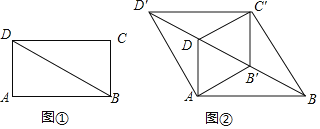
【題目】如圖![]() ,BD是矩形ABCD的對角線,
,BD是矩形ABCD的對角線,![]() ,
,![]() 將
將![]() 沿射線BD方向平移到
沿射線BD方向平移到![]() 的位置,使
的位置,使![]() 為BD中點,連接
為BD中點,連接![]() ,
,![]() ,
,![]() ,
,![]() ,如圖
,如圖![]() .
.
![]() 求證:四邊形
求證:四邊形![]() 是菱形;
是菱形;
![]() 四邊形
四邊形![]() 的周長為______;
的周長為______;
![]() 將四邊形
將四邊形![]() 沿它的兩條對角線剪開,用得到的四個三角形拼成與其面積相等的矩形,直接寫出所有可能拼成的矩形周長.
沿它的兩條對角線剪開,用得到的四個三角形拼成與其面積相等的矩形,直接寫出所有可能拼成的矩形周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角三角形![]() 中,
中,![]() ,
,![]() .點
.點![]() 是直線
是直線![]() 上一個動點(點
上一個動點(點![]() 不與點
不與點![]() ,
,![]() 重合),連接
重合),連接![]() ,在線段
,在線段![]() 的延長線上取一點
的延長線上取一點![]() ,使得
,使得![]() .過點
.過點![]() 作
作![]() ,交直線
,交直線![]() 于點
于點![]() .
.

(1)如圖1,當點![]() 在線段
在線段![]() 上時,若
上時,若![]() ,則
,則![]() _________;
_________;
(2)當點![]() 在線段
在線段![]() 的延長線上時,在圖2中依題意補全圖形,并判斷
的延長線上時,在圖2中依題意補全圖形,并判斷![]() 與
與![]() 有怎樣的數量關系,寫出你的結論,并證明;
有怎樣的數量關系,寫出你的結論,并證明;
(3)在點![]() 運動的過程中,直接寫出
運動的過程中,直接寫出![]() 與
與![]() 的數量關系為_________.
的數量關系為_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
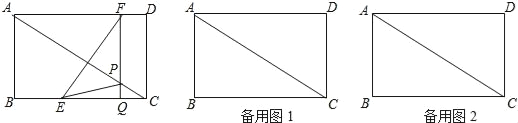
【題目】如圖,在矩形ABCD中,AB=6cm,BC=8cm,如果點E由點B出發沿BC方向向點C勻速運動,同時點F由點D出發沿DA方向向點A勻速運動,它們的速度分別為每秒2cm和1cm,FQ⊥BC,分別交AC、BC于點P和Q,設運動時間為t秒(0<t<4).
(1)連接EF,若運動時間t= 時,EF⊥AC;
(2)連接EP,當△EPC的面積為3cm2時,求t的值;
(3)若△EQP∽△ADC,求t的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com