解(1)

;0≤x≤1.
(2)①∵
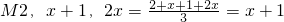
.
∵2x-(x+1)=x-1.
當x≥1時,則min{2,x+1,2x}=2,則x+1=2,∴x=1.
當x<1時,則min{2,x+1,2x}=2x,則x+1=2x,∴x=1(舍去)
綜上所述:x=1.
②a=b=c.理由如下:
∵
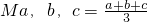
,
如果min{a,b,c}=c,則a≥c,b≥c.
則有
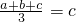
,即a+b-2c=0.
∴(a-c)+(b-c)=0.
又a-c≥0,b-c≥0,∴a-c=0,且b-c=0.
∴a=b=c.
其他情況同理可證,故a=b=c.
③根據題意得:
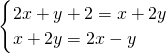
,
解得:
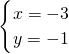
則x+y=-3-1=-4.
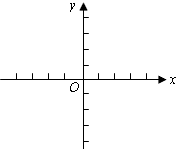
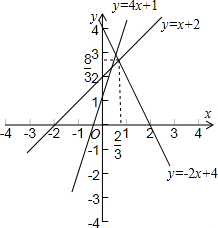
(3)作出圖象(如圖所示),由圖象知min{4x+1,x+2,-2x+4}的最大值為

.
分析:(1)
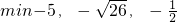
就是括號內的三個數中的最小的一個,據此即可確定;
min{2,2x+2,4-2x}=2,則2x+2≥2,且4-2x≥2,兩個式子同時成立,據此即可求得x的范圍;
(2)①M{2,x+1,2x}=
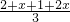
=x+1,若M{2,x+1,2x}=min{2,x+1,2x},則x+1是2、x+1、2x中最小的一個,即:x+1≤2且x+1≤2x,據此即可求得x的值;
②根據①可以得到結論:當三個數的平均數等于三個數中的最小的數,則這幾個數相等,據此即可寫出;
③根據結論,三個數相等,即可求得x,y的值,從而求得x+y的值;
(3)首先作出三個函數的圖象,min{4x+1,x+2,-2x+4}的最大值為三個函數的圖象的交點中,橫坐標最大的點的縱坐標就是所求的值.
點評:本題是一次函數與平均數,最小值函數相結合的題目,正確理解(1)中得到的結論是關鍵.

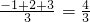 ,min{-1,2,3}=-1,min{-1,2,a}=
,min{-1,2,3}=-1,min{-1,2,a}=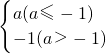

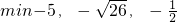 =______;
=______; ;0≤x≤1.
;0≤x≤1.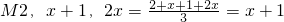 .
.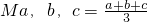 ,
,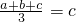 ,即a+b-2c=0.
,即a+b-2c=0.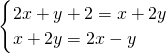 ,
,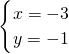
 .
.
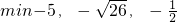 就是括號內的三個數中的最小的一個,據此即可確定;
就是括號內的三個數中的最小的一個,據此即可確定;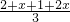 =x+1,若M{2,x+1,2x}=min{2,x+1,2x},則x+1是2、x+1、2x中最小的一個,即:x+1≤2且x+1≤2x,據此即可求得x的值;
=x+1,若M{2,x+1,2x}=min{2,x+1,2x},則x+1是2、x+1、2x中最小的一個,即:x+1≤2且x+1≤2x,據此即可求得x的值;

 名校課堂系列答案
名校課堂系列答案
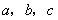 ,用
,用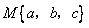 表示這三個數的平均數,用
表示這三個數的平均數,用 表示這三個數中最小的數.例如:
表示這三個數中最小的數.例如: ;
;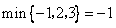 ;
;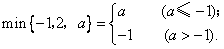 解決下列問題:
解決下列問題: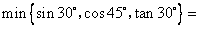 ______;
______;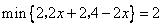 ,則x的取值范圍為
,則x的取值范圍為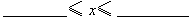 .
. ,求x;
,求x; 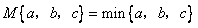 ,那么______ (填
,那么______ (填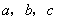 的大小關系)”.證明你發現的結論;
的大小關系)”.證明你發現的結論; 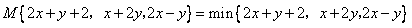 ,則
,則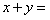 ______ .
______ .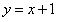 ,
,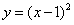 ,
,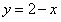 的圖象(不需列表描點).通過觀察圖象,
的圖象(不需列表描點).通過觀察圖象, 的最大值為______ .
的最大值為______ .