
【題目】已知E、F分別為正方形ABCD的邊BC、CD上的點,且∠EAF=45°.
(1)如圖①求證:BE+DF=EF;
(2)連接BD分別交AE、AF于M、N,
①如圖②,若AB=6![]() ,BM=3,求MN.
,BM=3,求MN.
②如圖③,若EF∥BD,求證:MN=CE.

【答案】(1)證明見解析;(2)①5;②證明見解析.
【解析】
(1)延長CB到G,使GB=DF,連接AG,求證△ABG≌△ADF,得∠3=∠2,AG=AF,進而求證△AGE≌△AFE,可得GB+BE=EF,所以DF+BE=EF.
(2)①如圖2,把△ABM繞點A逆時針旋轉90°得到△ADM′,連接NM′.就可以得出△ABM≌△ADM′,就有∠BAM=∠DAM′,就可以得出△AMN≌△AM′N就可以得出MN=M′N,由勾股定理就可以得出結論MN2=DN2+BM2;
②設正方形ABCD的邊長為a,求出MN,EC即可判斷;
(1)證明:證明:延長CB到G,使GB=DF,連接AG(如圖1),
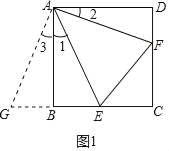
∵AB=AD,∠ABG=∠D=90°,GB=DF,
∴△ABG≌△ADF(SAS),
∴∠3=∠2,AG=AF,
∵∠BAD=90°,∠EAF=45°,
∴∠1+∠2=45°,
∴∠GAE=∠1+∠3=45°=∠EAF,
∵AE=AE,∠GAE=∠EAF,AG=AF,
∴△AGE≌△AFE(SAS),
∴GB+BE=EF,
∴DF+BE=EF;
(2)①解:如圖2,在正方形ABCD中,AB=AD,∠BAD=90°,
∴∠ABM=∠ADN=45°.
把△ABM繞點A逆時針旋轉90°得到△ADM'.連結NM'.
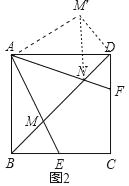
∴△ABM≌△ADM′(旋轉不變性),
∴DM'=BM,AM'=AM,∠ADM'=∠ABM=45°,∠DAM'=∠BAM.
∴∠ADB+∠ADM′=45°+45°=90°,
即∠NDM′=90°.
∵∠EAF=45°,
∴∠BAM+∠DAN=45°,
∴∠DAM′+∠DAF=45°,
即∠M′AN=45°,
∴∠M'AN=∠MAN.
在△AMN和△AM′N中
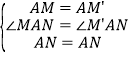 ,
,
∴△AMN≌△AM′N(SAS),
∴M'N=MN.
∵∠NDM′=90°,
∴M'N2=DN2+DM'2,
∴MN2=DN2+BM2;
設MN=x,則DN=12﹣3﹣x=9﹣x,
∴x2=33+(9﹣x)2,
∴x=5,
∴NM=5;
②證明:如圖3中,設正方形ABCD的邊長為a.
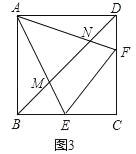
∵EF∥BD,
∴∠CEF=∠CBD=45°,∠CFE=∠CDB=45°,
∴∠CEF=∠CFE=45°,
∴CE=CF,
∴BE=DF,
∵AB=AD,∠ABE=∠ADF,BE=DF,
∴△ABE≌△ADF(SAS),
∴∠BAE=∠DAF,
∵∠EAF=45°,
∴∠BAE=∠DAF=22.5°,
∴∠AEB=∠BME=67.5°,
∴BM=BE,同理可證:DN=DF,
∴BM=DN=BE=DF,設BM=x,則MN=![]() x,
x,
∴2x+![]() x=
x=![]() a,
a,
∴x=(![]() ﹣1)a,
﹣1)a,
∴MN=(2﹣![]() )a,EC=BC﹣BE=(2﹣
)a,EC=BC﹣BE=(2﹣![]() )a,
)a,
∴MN=EC.


科目:初中數學 來源: 題型:
【題目】如圖,用火柴棒擺出一列正方形圖案,第①個圖案用了 4 根,第②個圖案用了 12 根,第③個圖案用了 24 根,按照這種方式擺下去,擺出第⑥個圖案用火柴棒的根數是( )

A. 84 B. 81 C. 78 D. 76
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上點![]() 在原點的左邊,到原點的距離為4,點
在原點的左邊,到原點的距離為4,點![]() 在原點右邊,從點
在原點右邊,從點![]() 走到點
走到點![]() ,要經過16個單位長度.
,要經過16個單位長度.
(1)寫出![]() 、
、![]() 兩點所對應的數;
兩點所對應的數;
(2)若點![]() 也是數軸上的點,點
也是數軸上的點,點![]() 到點
到點![]() 的距離是點
的距離是點![]() 到原點距離的3倍,求
到原點距離的3倍,求![]() 對應的數;
對應的數;
(3)已知點![]() 從點
從點![]() 開始向右出發,速度每秒1個單位長度,同時
開始向右出發,速度每秒1個單位長度,同時![]() 從
從![]() 點開始向右出發,速度每秒2個單位長度,設線段
點開始向右出發,速度每秒2個單位長度,設線段![]() 的中點為
的中點為![]() ,線段
,線段![]() 的值是否會發生變化?若會,請說明理由,若不會,請求出求其值.
的值是否會發生變化?若會,請說明理由,若不會,請求出求其值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面內的兩條直線有相交和平行兩種位置關系.




(1)如圖1,若![]() ,點
,點![]() 在
在![]() 外部,則有
外部,則有![]() ,又可證
,又可證![]() ,得
,得![]() ,將點
,將點![]() 移到
移到![]() 內部,如圖2,以上結論是否成立?若成立,說明理由;若不成立,則
內部,如圖2,以上結論是否成立?若成立,說明理由;若不成立,則![]() 之間有何數量關系?請證明你的結論;
之間有何數量關系?請證明你的結論;
(2)在如圖2中,將直線![]() 繞點
繞點![]() 逆時針方向旋轉一定角度交直線
逆時針方向旋轉一定角度交直線![]() 于點
于點![]() 如圖3,則
如圖3,則![]()
![]() 之間有何數量關系? (不需證明);
之間有何數量關系? (不需證明);
(3)根據(2)的結論,求如圖4中![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在四邊形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,點P從點A出發,沿折線ABCD方向以3cm/s的速度勻速運動;點Q從點D出發,沿線段DC方向以2cm/s的速度勻速運動. 已知兩點同時出發,當一個點到達終點時,另一點也停止運動,設運動時間為t(s).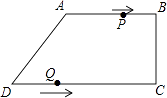
(1)求CD的長;
(2)當四邊形PBQD為平行四邊形時,求四邊形PBQD的周長;
(3)在點P、Q的運動過程中,是否存在某一時刻,使得△BPQ的面積為20cm2?若存在,請求出所有滿足條件的t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰直角△ABC中,AC=BC>3,點M在AC上,點N在CB的延長線上,MN交AB于點O,且AM=BN=3,則S△AMO與S△BNO的差是( )
A.9
B.4.5
C.0
D.無法確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,![]() ,點
,點![]() 在射線
在射線![]() 上,
上,![]() .
.

(1)如圖 1,若![]() ,求
,求![]() 的度數;
的度數;
(2)把“![]() °”改為“
°”改為“![]() ”,射線
”,射線![]() 沿射線
沿射線![]() 平移,得到
平移,得到![]() ,其它條件不變(如 圖 2 所示),探究
,其它條件不變(如 圖 2 所示),探究![]() 的數量關系;
的數量關系;
(3)在(2)的條件下,作![]() ,垂足為
,垂足為![]() ,與
,與![]() 的角平分線
的角平分線![]() 交于點
交于點![]() ,若
,若![]() , 用含 α 的式子表示
, 用含 α 的式子表示![]() (直接寫出答案).
(直接寫出答案).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com