【題目】2015年2月28日，前央視知名記者柴靜推出了關于霧霾的紀錄片——《穹頂之下》，引起了極大的反響．某市準備加大對霧霾的治理力度，2015年第一季度投入資金
萬元，第二季度和第三季度計劃共投入資金
萬元，求這兩個季度計劃投入資金的平均增長率．設這兩個季度計劃投入資金的平均增長率為
，根據題意可列方程為__________.
科目：初中數學 來源： 題型：
【題目】下表是2019年三月份某居民小區隨機抽取20戶居民的用水情況：
用水量/噸 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
戶數 | 2 | 4 | m | 4 | 3 | 0 | 1 |
（1）求出m＝ ，補充畫出這20戶家庭三月份用電量的條形統計圖；
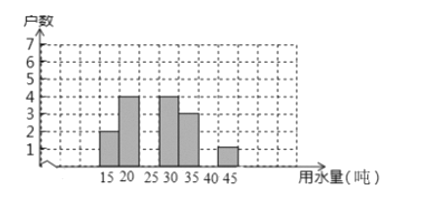
（2）據上表中有關信息，計算或找出下表中的統計量，并將結果填入表中：
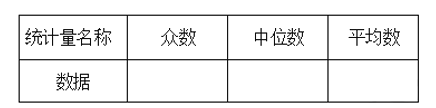
（3）為了倡導“節約用水，綠色環保”的意識，臺州市自來水公司實行“梯級用水、分類計費”，價格表如下：
如果該小區有500戶家庭，根據以上數據，請估算該小區三月份有多少戶家庭在ⅠI級標準？并估算這些級用水戶的總水費是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線
與x軸交于點A、B兩點（A點在B點左側），與y軸交于點C（0，-3），對稱軸是直線x=1，直線BC與拋物線的對稱軸交于點D．
（1）求出拋物線的函數表達式；
（2）設點E時拋物線上一點，且S△ABE=
S△ABC，求tan∠ECO的值；
（3）點P在拋物線上，點Q在拋物線對稱軸上，若以B、C、P、Q為頂點的四邊形是平行四邊形，求點P坐標。
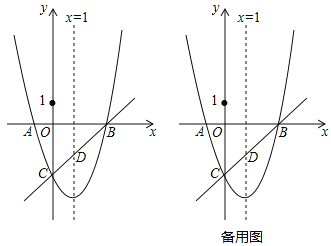
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線
上有兩點M(m+1，a)、N(m，b).
(1)當a＝－1，m＝1時，求拋物線的解析式；
(2)用含a、m的代數式表示b和c；
(3)當a＜0時，拋物線滿足
，
，
，
求a的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】校車安全是近幾年社會關注的重大問題，安全隱患主要是超速和超載，某中學數學活動小組設計了如下檢測公路上行駛的汽車速度的實驗：先在公路旁邊選取一點C，再在筆直的車道l上確定點D，使CD與l垂直，測得CD的長等于24米，在l上點D的同側取點A、B，使∠CAD＝30°，∠CBD＝60°．
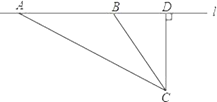
（1）求AB的長（結果保留根號）；
（2）已知本路段對校車限速為45千米/小時，若測得某輛校車從A到B用時2秒，這輛校車是否超速？說明理由．（參考數據：
≈1.7，
≈1.4）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，
、
、
、
為矩形的四個頂點，
，
，動點
、
分別從點、同時出發，點以
的速度向點移動，一直到達為止，點以
的速度向移動．
、兩點從出發開始到幾秒？四邊形
的面積為
；
、兩點從出發開始到幾秒時？點和點的距離是
．
查看答案和解析>>
科目：初中數學 來源： 題型：
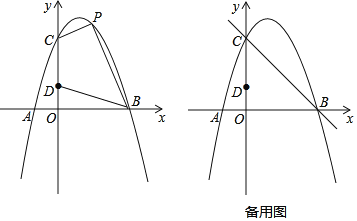
【題目】如圖，對稱軸為直線x＝1的拋物線經過A（﹣1，0）、C（0，3）兩點，與x軸的另一個交點為B，點D在y軸上，且OB＝3OD
（1）求該拋物線的表達式；
（2）設該拋物線上的一個動點P的橫坐標為t
①當0＜t＜3時，求四邊形CDBP的面積S與t的函數關系式，并求出S的最大值；
②點Q在直線BC上，若以CD為邊，點C、D、Q、P為頂點的四邊形是平行四邊形，請求出所有符合條件的點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
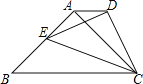
【題目】如圖，等腰Rt△ABC，∠BAC＝90°，BC＝
，E為AB上一點，以CE為斜邊作等腰Rt△CDE，連接AD，若∠ACE＝30°，則AD的長為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知關于x的一元二次方程x2﹣2tx+t2﹣2t+4＝0．
（1）當t＝3時，解這個方程；
（2）若m，n是方程的兩個實數根，設Q＝（m﹣2）（n﹣2），試求Q的最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
