
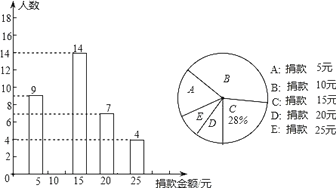
【題目】某校八年級全體同學參加了某項捐款活動,隨機抽查了部分同學捐款的情況統計如圖所示
(1)本次共抽查學生____人,并將條形圖補充完整;
(2)捐款金額的眾數是_____,平均數是_____;
(3)在八年級700名學生中,捐款20元及以上(含20元)的學生估計有多少人?
【答案】(1)50;補圖見解析;(2)10,13.1;(3)154人.
【解析】
(1)有題意可知,捐款15元的有14人,占捐款總人數的28%,由此可得總人數,將捐款總人數減去捐款5、15、20、25元的人數可得捐10元的人數;
(2)從條形統計圖中可知,捐款10元的人數最多,可知眾數,將50人的捐款總額除以總人數可得平均數;
(3)由抽取的樣本可知,用捐款20及以上的人數所占比例估計總體中的人數.
(1)本次抽查的學生有:14÷28%=50(人),
則捐款10元的有50﹣9﹣14﹣7﹣4=16(人),補全條形統計圖圖形如下:
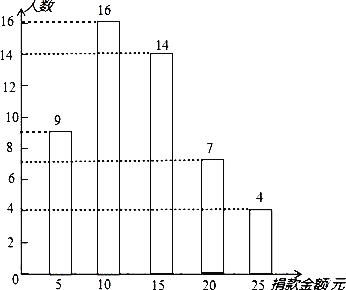
故答案為:50;
(2)由條形圖可知,捐款10元人數最多,故眾數是10;
這組數據的平均數為:![]() =13.1;
=13.1;
故答案為:10,13.1.
(3)捐款20元及以上(含20元)的學生有:![]() ×700=154(人);
×700=154(人);


科目:初中數學 來源: 題型:
【題目】如圖,A,B,C三點在數軸上,點A表示的數為-10,點B表示的數為14,點C到點A和點B之間的距離相等.
![]()
(1)求A,B兩點之間的距離;
(2)求C點對應的數;
(3)甲、乙分別從A,B兩點同時相向運動,甲的速度是1個單位長度/s,乙的速度是2個單位長度/s,求相遇點D對應的數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在梯形ABCD中,AD∥BC,∠C=90°,DC=5,以CD為半徑的⊙C與以AB為半徑的⊙B相交于點E、F,且點E在BD上,聯結EF交BC于點G.
(1)設BC與⊙C相交于點M,當BM=AD時,求⊙B的半徑;
(2)設BC=x,EF=y,求y關于x的函數關系式,并寫出它的定義域;
(3)當BC=10時,點P為平面內一點,若⊙P與⊙C相交于點D、E,且以A、E、P、D為頂點的四邊形是梯形,請直接寫出⊙P的面積.(結果保留π)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD內部有若干個點,用這些點以及正方形ABCD的頂點A、B、C、D把原正方形分割成一些三角形(互相不重疊):
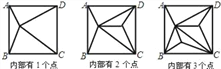
(1)填寫下表:
正方形ABCD內點的個數 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的個數 | 4 | 6 | … |
(2)原正方形能否被分割成2008個三角形?若能,求此時正方形ABCD內部有多少個點?若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=x﹣4與x軸交于點A,以OA為斜邊在x軸上方作等腰Rt△OAB,并將Rt△AOB沿x軸向右平移,當點B落在直線y=x﹣4上時,Rt△OAB掃過的面積是__.
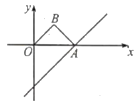
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(11·湖州)(本小題10分)
如圖,已知E、F分別是□ABCD的邊BC、AD上的點,且BE=DF。
⑴求證:四邊形AECF是平行四邊形;
⑵若BC=10,∠BAC=90°,且四邊形AECF是菱形,求BE的長。
查看答案和解析>>
科目:初中數學 來源: 題型:
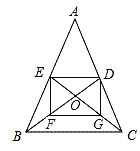
【題目】如圖,△ABC的中線BD,CE交于點O,F,G分別是BO,CO的中點.
(1)填空:四邊形DEFG是 四邊形.
(2)若四邊形DEFG是矩形,求證:AB=AC.
(3)若四邊形DEFG是邊長為2的正方形,試求△ABC的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
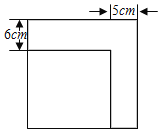
【題目】如圖,小剛將一個正方形紙片剪去一個寬為5cm的長條后,再從剩下的長方形紙片上剪去一個寬為6cm的長條.如果兩次剪下的長條面積正好相等,求兩個所剪下的長條的面積之和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com