【題目】已知一次函數
的圖象與反比例函數
的圖象交于點
，與
軸交于點
，若
，且
.
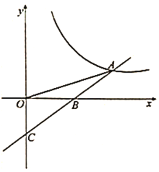
（1）求反比例函數與一次函數的表達式；
（2）若點
為x軸上一點，
是等腰三角形，求點的坐標.
【答案】（l）
，
；（2）
、
，
，
【解析】
（1）根據
可計算出A點的縱坐標，進而利用勾股定理計算出A點的橫坐標，代入可得一次函數和反比例函數的解析式.
（2）根據題意可得有三種情況，一種是AB為底，一種是AB為腰，以A為頂點，一種是AB為腰，以B為頂點.
（l）過點
作
軸于點
∵
∴
∴
∵
∴
在
中，
∴
∴
∵
經過點 ∴
∴
∴反比例函數表達式為
∵
經過點，點
∴
解得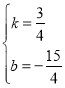
∴一次函數表達式為
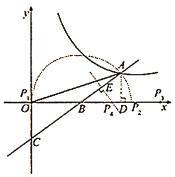
（2）本題分三種情況
①當以
為腰，且點為頂角頂點時，可得點
的坐標為、
②當以為腰，且以點為頂角頂點時，點關于
的對稱點即為所求的點
③當以為底時，作線段的中垂線交
軸于點
，交于點
，則點即為所求
由（1）得，
在
中，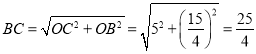
∵
∴
∴
∴
∴
∴
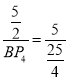名校課堂系列答案科目：初中數學 來源： 題型：
【題目】如圖，在矩形ABCD中，AB=4，AD=3，矩形內部有一動點P滿足S△PAB=
S矩形ABCD，則點P到A、B兩點的距離之和PA+PB的最小值為______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC 中，AB=AC，點 M 在 BA 的延長線上，點 N 在 BC 的延長線上，過點 C 作CD∥AB 交∠CAM 的平分線于點 D．
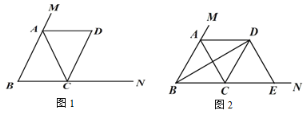
（1）如圖 1，求證：四邊形 ABCD 是平行四邊形；
（2）如圖 2，當∠ABC=60°時，連接 BD，過點 D 作 DE⊥BD，交 BN 于點 E，在不添加任何輔助線的情況下，請直接寫出圖 2 中四個三角形（不包含△CDE），使寫出的每個三角形的面積與△CDE 的面積相等．
查看答案和解析>>
科目：初中數學 來源： 題型：
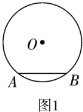
【題目】（1）如圖1，
、
是
上的兩個點，點
在上，且
是直角三角形，的半徑為1．
①請在圖1中畫出點的位置；
②當
時，
；
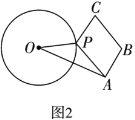
（2）如圖2，的半徑為5，、為外固定兩點（
、、三點不在同一直線上），且
，為上的一個動點（點不在直線
上），以
和為鄰邊作平行四邊形
，求
最小值并確定此時點的位置；
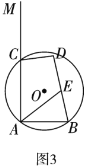
（3）如圖3，、是上的兩個點，過點作射線
，
交于點
，若
，
，點
是平面內的一個動點，且
，
為
的中點，在點的運動過程中，求線段
長度的最大值與最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
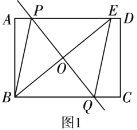
【題目】（1）如圖1，矩形
中，點
、
分別在線段
、
上，點
與點
關于
對稱，點在線段上，連接
、
、交
于點
．求證：四邊形
是菱形；
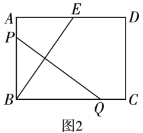
（2）如圖2，矩形中，
，點、分別在線段
、上，點與點關于對稱，點在線段上，
，求
的長；
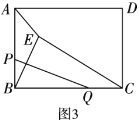
（3）如圖3，有一塊矩形空地，
，
，點是一個休息站且在線段上，
，點在線段上，現要在點關于對稱的點處修建一口水井，并且修建水渠
和
，以便于在四邊形空地
上種植花草，余下部分貼上地磚．種植花草的四邊形空地的面積是否存在最小值，若存在，請求出最小值，若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校有1500名學生，小明想了解全校學生每月課外閱讀書籍的數量情況，隨機抽取了部分學生，得到如統計圖：
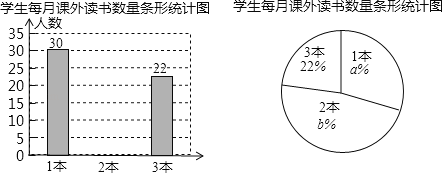
（1）一共抽查了多少人？
（2）每月課外閱讀書籍數量是1本的學生對應的圓心角度數是多少？
（3）估計該校全體學生每月課外閱讀書籍的總量大約是多少本？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某學校八、九兩個年級各有學生180人，為了解這兩個年級學生的體質健康情況，進行了抽樣調查，具體過程如下：
收集數據
從八、九兩個年級各隨機抽取20名學生進行體質健康測試，測試成績（百分制）如下：
八年級 | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
九年級 | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
整理、描述數據
將成績按如下分段整理、描述這兩組樣本數據：
成績（x） | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
八年級人數 | 0 | 0 | 1 | 11 | 7 | 1 |
九年級人數 | 1 | 0 | 0 | 7 | 10 | 2 |
（說明：成績80分及以上為體質健康優秀，70～79分為體質健康良好，60～69分為體質健康合格，60分以下為體質健康不合格）
分析數據
兩組樣本數據的平均數、中位數、眾數、方差如表所示：
年級 | 平均數 | 中位數 | 眾數 | 方差 |
八年級 | 78.3 | 77.5 | 75 | 33.6 |
九年級 | 78 | 80.5 | a | 52.1 |
（1）表格中a的值為______；
（2）請你估計該校九年級體質健康優秀的學生人數為多少？
（3）根據以上信息，你認為哪個年級學生的體質健康情況更好一些？請說明理由．（請從兩個不同的角度說明推斷的合理性）
查看答案和解析>>
科目：初中數學 來源： 題型：
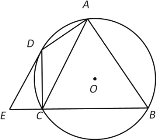
【題目】如圖，四邊形ABCD內接于⊙O，∠BAD＝90°，點E在BC的延長線上，且∠DEC＝∠BAC．
（1）求證：DE是⊙O的切線；
（2）若AC∥DE，當AB＝12，CE＝3時，求AC的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】數學概念
在兩個等腰三角形中，如果其中一個三角形的底邊長和底角的度數分別等于另一個三角形的腰長和頂角的度數，那么稱這兩個等腰三角形互為姊妹三角形．
概念理解
（1）如圖①，在△ABC中，AB＝AC，請用直尺和圓規作出它的姊妹三角形（保留作圖痕跡，不寫作法）．
特例分析
（2）①在△ABC中，AB＝AC，∠A＝30°，
，求它的姊妹三角形的頂角的度數和腰長；
②如圖②，在△ABC中，AB＝AC，D是AC上一點，連接BD．若△ABC與△ABD互為姊妹三角形，且△ABC∽△BCD，則∠A＝ °．
深入研究
（3）下列關于姊妹三角形的結論：
①每一個等腰三角形都有姊妹三角形；
②等腰三角形的姊妹三角形是銳角三角形；
③如果兩個等腰三角形互為姊妹三角形，那么這兩個三角形可能全等；
④如果一個等腰三角形存在兩個不同的姊妹三角形，那么這兩個三角形也一定互為姊妹三角形．
其中所有正確結論的序號是 ．
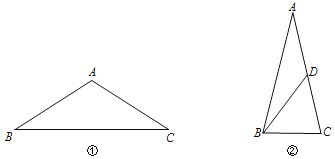
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com