
分析 根據三次項系數為1可設另一個因式為(x+k),將原式變形為x3+mx2+nx+p=(x-1)(x+4)(x+k)=x3+(k+3)x2+(3k-4)x-4k,可得$\left\{\begin{array}{l}{m=k+3}\\{n=3k-4}\\{p=-4k}\end{array}\right.$,代入2m-2n-p+86可得答案.
解答 解:∵x-1,x+4均為多項式x3+mx2+nx+p的因式,且三次項系數為1,
∴設另一個因式為(x+k),
則x3+mx2+nx+p=(x-1)(x+4)(x+k)=x3+(k+3)x2+(3k-4)x-4k,
∴$\left\{\begin{array}{l}{m=k+3}\\{n=3k-4}\\{p=-4k}\end{array}\right.$,
∴2m-2n-p+86=2(k+3)-2(3k-4)+4k+86
=2k+6-6k+8+4k+86
=100,
故答案為:100.
點評 本題主要考查因式分解的意義,根據系數設另一個因式,從而變形將待求式子的未知數化為統一未知數是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
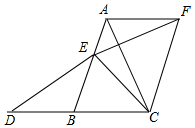 如圖,在△ABC中,點E在線段AB上,點D在射線CB上,且ED=EC,將△BCE繞點C順時針旋轉60°至△ACF(點B、E的對應點分別為點A、F),連接EF.
如圖,在△ABC中,點E在線段AB上,點D在射線CB上,且ED=EC,將△BCE繞點C順時針旋轉60°至△ACF(點B、E的對應點分別為點A、F),連接EF.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
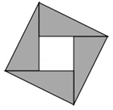 如圖是“趙爽弦圖”,由4個全等的直角三角形拼成的圖形,若大正方形的面積是13,小正方形的面積是1,設直角三角形較長直角邊為a,較短直角邊為b,則a+b的值是5.
如圖是“趙爽弦圖”,由4個全等的直角三角形拼成的圖形,若大正方形的面積是13,小正方形的面積是1,設直角三角形較長直角邊為a,較短直角邊為b,則a+b的值是5.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 下面是某地區近5年城鎮居民與農村居民人均收入增速對比表:
下面是某地區近5年城鎮居民與農村居民人均收入增速對比表:| 年份 增速 類別 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 |
| 城鎮 | 8.5 | 13.6 | 12.5 | 9.3 | 11.5 |
| 農村 | 10 | 10.5 | 14.2 | 12.5 | 14.6 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com