【題目】若一個多邊形從一個頂點，只可以引三條對角線，則它是( )邊形．
A. 五 B. 六 C. 七 D. 八
天天向上口算本系列答案科目：初中數學 來源： 題型：
【題目】把下列各數填在相應的表示集合的大括號內： 
，﹣0. 
，﹣（﹣2），﹣ 
，1.732， 
，0， 
，1.1010010001…（每兩個1之間依次多一個0） 整 數{…}
正分數{…}
無理數{…}
實 數 {…}．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】經統計，2016年除夕夜觀看春晚直播的觀眾約達10.3億人，用科學記數法表示10.3億正確的是（ ）
A.1.03×109
B.1.03×1010
C.10.3×109
D.103×108
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某班同學參加環保知識競賽，將學生的成績（得分取整數）進行整理后分成五組
繪成條形統計圖如圖所示，圖中從左到右各小組小長方形的高的比是1:2:6:4:2，最右邊一組的人數是6，結合圖形提供的信息解答下列問題：
（1）該班共有多少名同學參賽？
（2）成績落在哪組數據范圍內的人數最多，
是多少？
（3）求成績在60分以下（含60分）的人數是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，李明同學在東西方向的濱海路A處，測得海中燈塔P在北偏東60°方向上，他向東走400米至B處，測得燈塔P在北偏東30°方向上，求燈塔P到濱海路的距離．（結果保留根號）
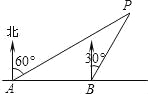
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小紅和小明在研究一個數學問題：已知AB∥CD，AB和CD都不經過點E，探索∠E與∠A，∠C的數量關系．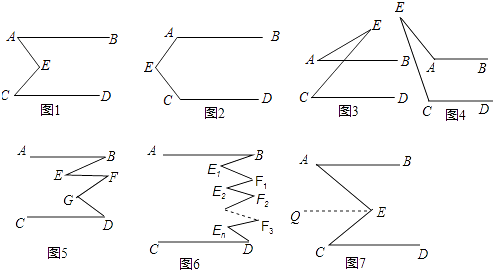 
（1）發現：在圖1中，小紅和小明都發現：∠AEC=∠A+∠C； 小紅是這樣證明的：如圖7過點E作EQ∥AB．
∴∠AEQ=∠A（）
∵EQ∥AB，AB∥CD．
∴EQ∥CD（）
∴∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C 即∠AEC=∠A+∠C．
小明是這樣證明的：如圖7過點E作EQ∥AB∥CD．
∴∠AEQ=∠A，∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C即∠AEC=∠A+∠C
請在上面證明過程的橫線上，填寫依據：
兩人的證明過程中，完全正確的是 ．
（2）嘗試： ①在圖2中，若∠A=110°，∠C=130°，則∠E的度數為；
②在圖3中，若∠A=20°，∠C=50°，則∠E的度數為 ．
（3）探索： 裝置圖4中，探索∠E與∠A，∠C的數量關系，并說明理由．
（4）猜想： 如圖5，∠B、∠D、∠E、∠F、∠G之間有什么關系？（直接寫出結論）
（5）如圖6，你可以得到什么結論？（直接寫出結論）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
