
【題目】已知:在等邊△ABC中, AB=![]() , D,E分別是AB,BC的中點(如圖1).若將△BDE繞點B逆時針旋轉,得到△BD1E1,設旋轉角為α(0°<α<180°),記射線CE1與AD1的交點為P.
, D,E分別是AB,BC的中點(如圖1).若將△BDE繞點B逆時針旋轉,得到△BD1E1,設旋轉角為α(0°<α<180°),記射線CE1與AD1的交點為P.
(1)判斷△BDE的形狀;

(2)在圖2中補全圖形,
①猜想在旋轉過程中,線段CE1與AD1的數量關系并證明;
②求∠APC的度數;
(3)點P到BC所在直線的距離的最大值為________.(直接填寫結果)

 、
、
圖2 備用
【答案】(1)等邊三角形;
(2)①見解析;②見解析.
【解析】
(1)由D、E分別是AB、BC的中點得到![]() ,
,![]() ,加上
,加上![]() 為等邊三角形,則
為等邊三角形,則![]() ,
,![]() ,所以
,所以![]() ,于是可判斷
,于是可判斷![]() 為等邊三角形;
為等邊三角形;
(2)①根據旋轉的性質得![]() 為等邊三角形,則
為等邊三角形,則![]() ,
,![]() ,而
,而![]() ,所以∠D1BA=∠E1BC,則可證明△ABD1≌△CBE1,所以CE1=AD1;
,所以∠D1BA=∠E1BC,則可證明△ABD1≌△CBE1,所以CE1=AD1;
②由△ABD1≌△CBE1,可得到∠D1AB=∠E1CB,即可得到∠APC=∠ABC;
(3)由于![]() ,則可判斷點P、D1、B、E1共圓,于是可判斷當
,則可判斷點P、D1、B、E1共圓,于是可判斷當![]() 時,點P到BC所在直線的距離的最大值,此時點E在AB上,然后利用含30度的直角三角形三邊的關系可得點P到BC所在直線的距離的最大值.
時,點P到BC所在直線的距離的最大值,此時點E在AB上,然后利用含30度的直角三角形三邊的關系可得點P到BC所在直線的距離的最大值.
解:
(1)等邊三角形.
(2)補全圖形如右圖.
①CE1=AD1.
∵ △ABC和△BD1E1為等邊三角形,
∴ BC=BA,BE1=BD1,∠ABC=∠D1BE1=60°.
∴ ∠ABC-∠ABE1 =∠D1BE1-∠ABE1.
即∠D1BA=∠E1BC.
∴ △ABD1≌△CBE1.
∴ CE1=AD1.
②∵ △ABD1≌△CBE1,
∴ ∠D1AB=∠E1CB.
又∵∠D1AB+∠APC=∠ABC+∠E1CB,
∴ ∠APC=∠ABC=60°.
(3)2.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,AB的垂直平分線MN交AC于點D,交AB于點E.
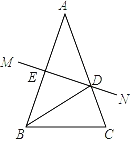
(1)若∠A=40°,求∠DBC的度數;
(2)若AE=6,△CBD的周長為20,求△ABC的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知⊙O的半徑為5,EF是長為8的弦,OG⊥EF于點G,點A在GO的延長線上,且AO=13.弦EF從圖1的位置開始繞點O逆時針旋轉,在旋轉過程中始終保持OG⊥EF,如圖2.
[發現]在旋轉過程中,
(1)AG的最小值是 ,最大值是 .
(2)當EF∥AO時,旋轉角α= .
[探究]若EF繞點O逆時針旋轉120°,如圖3,求AG的長.
[拓展]如圖4,當AE切⊙O于點E,AG交EO于點C,GH⊥AE于H.
(1)求AE的長.
(2)此時EH= ,EC= .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1, 在![]() 中,
中,![]() ,
,![]() .點O是BC的中點,點D沿B→A→C方向從B運動到C.設點D經過的路徑長為
.點O是BC的中點,點D沿B→A→C方向從B運動到C.設點D經過的路徑長為![]() ,圖1中某條線段的長為y,若表示y與x的函數關系的圖象大致如圖2所示,則這條線段可能是圖1中的 ( )
,圖1中某條線段的長為y,若表示y與x的函數關系的圖象大致如圖2所示,則這條線段可能是圖1中的 ( )

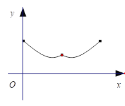
圖1 圖2
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=﹣x2+2x+3與x軸交于A,B兩點,點A在點B的左側.
(1)求A,B兩點的坐標和此拋物線的對稱軸;
(2)設此拋物線的頂點為C,點D與點C關于x軸對稱,求四邊形ACBD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】開學初,為豐富教師們的業余生活,我校組織所有教師前往重慶大劇院觀看演出。重慶大劇院的演出門票價格方案如下:1.票價根據座位區域不同定價不同,一區票價為120元/張,二區票價為100元/張;2.離退休教師各區均享受八折優惠。已知本次活動實到教師700人,若本次活動每人均購買二區票則需67200元。
(1)求參加本次活動的在職教師、離退休教師分別有多少人;
(2)為慶祝重陽節,重慶在大劇院調整了票價方案,將200張一區演出票票價每張降低了![]() 元,將全部二區演出票票價每張降低了
元,將全部二區演出票票價每張降低了![]() 元,離退休教師可在降價后仍享受八折優惠。若學校決定將200張一區演出票全部購入并優先發放給離退休教師和部分在職教師,其余教師均購買二區票,且校方希望總門票費用不超過66420元,求
元,離退休教師可在降價后仍享受八折優惠。若學校決定將200張一區演出票全部購入并優先發放給離退休教師和部分在職教師,其余教師均購買二區票,且校方希望總門票費用不超過66420元,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P為邊BC上一動點,PE⊥AB于E,PF⊥AC于F,M為EF中點,則AM的最小值是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在大課間活動中,同學們積極參加體育鍛煉,小龍在全校隨機抽取了一部分同學就“我最喜愛的體育項目”進行了一次調查(每位同學必選且只選一項)下面是他通過收集的數據繪制的兩幅不完整的統計圖,請你根據圖中提供的信息,解答以下問題:
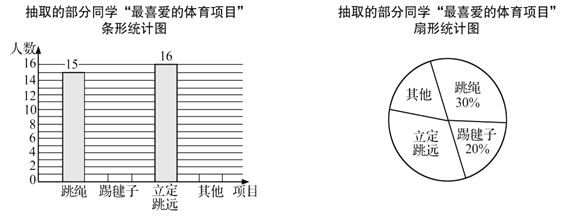
(1)小龍一共抽取了 名學生.
(2)補全條形統計圖.
(3)求“立定跳遠”部分對應的扇形圓心角的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com