【題目】已知A=a2-2ab+b2，B=a2+2ab+b2.
（1）求A+B;
（2）求
（A+B）；
（3）如果2A-3B+C=0,那么C的表達式是什么？
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，點A(0，a)，B(b，12－b)，C(2a－3，0)，0＜a＜b＜12，若OB平分∠AOC，且AB＝BC，則a＋b的值為（ ）
A. 9或12B. 9或11C. 10或11D. 10或12
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某童裝網店批發商批發一種童裝，平均每天可售出
件，每件盈利
元.經調查，如果每件童裝降價
元，那么平均每天就可多售出
件.
（1）設每件童裝降價
元，那么每天可售出多少件童裝？每件童裝的利潤是多少元？（用含的代數式表示）
（2）為了迎接“六一”兒童節，商家決定降價促銷、盡快減少庫存，又想保證平均每天盈利
元，求每件童裝應降價多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將一副直角三角尺的直角頂點C疊放在一起．
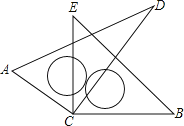
（1）若∠DCE＝35°，∠ACB＝ ；若∠ACB＝140°，則∠DCE＝ ；
（2）猜想∠ACB與∠DCE的大小有何特殊關系，并說明理由；
（3）若保持三角尺BCE（其中∠B＝45°）不動，三角尺ACD的CD邊與CB邊重合，然后將三角尺ACD（其中∠D＝30°）繞點C按逆時針方向任意轉動一個角度∠BCD．
設∠BCD＝α（0°＜α＜90°）
①∠ACB能否是∠DCE的4倍？若能求出α的值；若不能說明理由．
②當這兩塊三角尺各有一條邊互相垂直時直接寫出α的所有可能值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖是某學校草場一角，在長為b米，寬為a米的長方形場地中間，有并排兩個大小一樣的籃球場，兩個籃球場中間以及籃球場與長方形場地邊沿的距離都為c米．
（1）用代數式表示這兩個籃球場的占地面積．
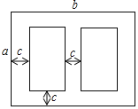
（2）當a=30，b=40，c=3時，計算出一個籃球場的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】由幾個相同的邊長為1的小立方塊搭成的幾何體的俯視圖如下圖，格中的數字表示該位置的小立方塊的個數．
(1)請在下面方格紙中分別畫出這個向何體的主視圖和左視圖．
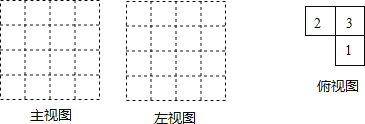
(2)根據三視圖；這個組合幾何體的表面積為 _________ 個平方單位．(包括底面積)
(3)若上述小立方塊搭成的幾何體的俯視圖不變，各位置的小立方塊個數可以改變(總數目不變)，則搭成這樣的組合幾何體中的表面積最大是為 _________ 個平方單位．(包括底面積)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①所示的是一個正方體的表面展開圖，將對應的正方體從如圖②所示的位置依次翻到第1格、第2格、第3格，這時正方體朝上的一面上的字是________．
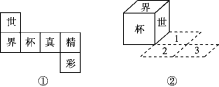
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，平行四邊形ABCD中，E，F是對角線BD上的兩點，如果添加一個條件使△ABE≌△CDF，則添加的條件不能是（ ）
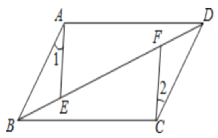
A. AE=CFB. BE=FDC. BF=DED. ∠1=∠2
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知O是AB上的一點，從O點引出射線OC、OE、OD，其中OE平分∠BOC.
（1）如圖1，若∠COD是直角，∠DOE=15°，求∠AOE的度數；
（2）如圖1，若∠AOC=∠BOD，∠DOE=15°，求∠AOE的度數；
（3）將圖1中的∠COD （∠COD仍是直角）繞頂點O順時針旋轉至圖2的位置，若∠AOC=
, ∠DOE=
，請猜想與之間存在什么樣的數量關系，寫出你的結論，并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
