科目：初中數學 來源： 題型：
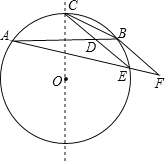
【題目】如圖示AB為⊙O的一條弦，點C為劣弧AB的中點，E為優弧AB上一點，點F在AE的延長線上，且BE=EF，線段CE交弦AB于點D．
①求證：CE∥BF；
②若BD=2，且EA：EB：EC=3：1：
，求△BCD的面積（注：根據圓的對稱性可知OC⊥AB）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為響應國家節能減排的號召，鼓勵居民節約用電，各省先后出臺了居民用電“階梯價格”制度，如下表是某省的電價標準(每月)．例如：方女士家5月份用電500度，電費＝180×0.6＋220×二檔電價＋100×三檔電價＝352元；李先生家5月份用電460度，交費316元．請問表中二檔電價、三檔電價各是多少？
階梯 | 電量 | 電價 |
一檔 | 0～180度 | 0.6元/度 |
二檔 | 181～400度 | 二檔電價 |
三檔 | 401度及以上 | 三檔電價 |
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】 正方形
的邊長為1，點
是
邊上的一個動點（與
不重合)，以
為頂點在所在直線的上方作
.
(1)當
經過點
時，
①請直接填空：
（可能，不可能）過
點；（圖1僅供分析）
②如圖2,在
上截取
，過
點作
垂直于直線
,垂足為點
，冊
于
，求證：四邊形
為正方形.
（2）當
不過點
時，設交邊
于
,且
.在
上存在點
,過
點作
垂直于直線
,垂足為點
，使得
，連接
，求四邊形
的最大面積.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】拋物線y=x2+bx+c與x軸交于A（1，0），B（m，0），與y軸交于C．
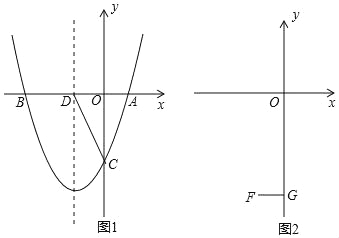
（1）若m=﹣3，求拋物線的解析式，并寫出拋物線的對稱軸；
（2）如圖1，在（1）的條件下，設拋物線的對稱軸交x軸于D，在對稱軸左側的拋物線上有一點E，使S△ACE=
S△ACD，求點E的坐標；
（3）如圖2，設F（﹣1，﹣4），FG⊥y于G，在線段OG上是否存在點P，使∠OBP=∠FPG？若存在，求m的取值范圍；若不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
